本文主要回顾归并排序,主要有如下内容:
- 白话说归并排序
- 归并排序的具体实现
- 归并排序的优化
白话说归并排序
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案merge在一起,即分而治之)。
归并排序将待排序数组A[1..n]分成两个各含n/2个元素的子序列,然后对这个两个子序列进行递归排序,最后将这两个已排序的子序列进行合并,即得到最终排好序的序列。
具体示例,比如下图中的序列:
首先,要想将该8个元素的序列进行排序,利用分而治之的想法,就可以不断的分解,分解到第三层的时候,每个子序列就只剩一个元素了,那此时就是有序的了。
可以看到8个元素的序列,可以分成3层,2^3 = 8,其实N个元素的序列就可以分为log(N)个层级;
其次另外一个问题,就是子序列有序了,如何merge成一个更大的有序的序列;比如下图左右两边都是有序的,如何merge
这个时候其实需要开辟一段辅助空间来,其实就是利用空间换取时间
merge过程图示: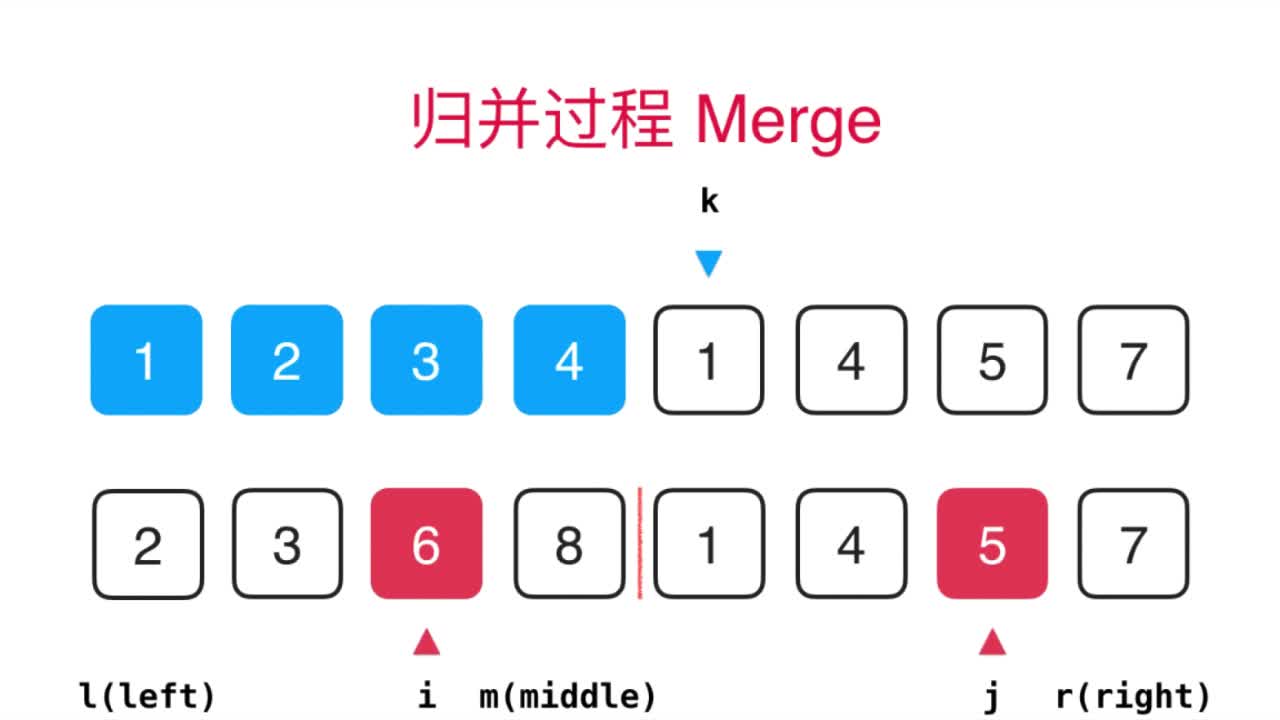
下面另外开辟一段辅助空间复制了一份待归并的2个序列,分别用了k指向待排序的序列的索引(l<=k<=r),i指向待归并的左边序列(l<=i<=mid),j指向右边待归并的序列(mid+1<=j<r).
通过上面的分析,我们比较直观地能感受到归并排序的时间复杂度为O( Nlog^N ),本文不做详细论证,有兴趣的同学可以查阅相关资料。
归并排序的具体实现
清单1 归并排序具体实现的头文件mergeSort.h1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
template<typename T>
void __merge(T a[], int l, int mid, int r)
{
T aux[r-l+1];
for(int i = l; i <= r; i++)
aux[i-l] = a[i];
int i = l;
int j = mid + 1;
for(int k = l; k <= r; k++)
{
if(i > mid)
{
a[k] = aux[j-l];
j++;
}
else if(j > r)
{
a[k] = aux[i-l];
i++;
}
else if(aux[i-l] < aux[j-l])
{
a[k] = aux[i-l];
i++;
}
else
{
a[k] = aux[j-l];
j++;
}
}
return;
}
template<typename T>
void __mergeSort(T a[], int l, int r)
{
if(l >= r)
return;
int mid = (l + r) / 2;
__mergeSort(a, l, mid);
__mergeSort(a, mid+1, r);
__merge(a, l, mid, r);
return;
}
template<typename T>
void mergeSort(T a[], int n)
{
__mergeSort(a, 0, n-1);
return;
}
清单2 main函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//#include "insertionSort.h"
//#include "shellSort.h"
using namespace std;
int main()
{
int n = 100;
cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
int *arr = SortTestHelper::generateRandomArray(n, 0, n);
int *arr1 = SortTestHelper::copyArray(arr, n);
int *arr2 = SortTestHelper::copyArray(arr, n);
// SortTestHelper::testSort("Shell Sort", shellSort, arr, n);
// //SortTestHelper::printArray(arr, n);
// SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
//SortTestHelper::printArray(arr1, n);
SortTestHelper::testSort("Merge Sort", mergeSort, arr2, n);
//SortTestHelper::printArray(arr2, n);
delete[] arr;
delete[] arr1;
delete[] arr2;
// n=100000;
// cout<<"Test for random array,size£º"<<n<<" range [0, "<<n<<"]."<<endl;
// arr = SortTestHelper::generateRandomArray(n, 0, n);
// arr1 = SortTestHelper::copyArray(arr, n);
// SortTestHelper::testSort("Shell Sort", shellSort, arr, n);
// //SortTestHelper::printArray(arr, n);
// SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
// delete[] arr;
// delete[] arr1;
return 0;
}
注意:SortTestHelper.h与插入排序中清单1头文件相同。
归并排序的优化
- 归并时判断,如果a[mid] <= a[mid+1],其实左右两边就已经有序了,此次就不需要归并了
- 递归结束的时间点,在序列剩下较小数量的时候可以采用直接插入排序进行优化
清单3:归并排序优化11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
template<typename T>
void __merge(T a[], int l, int mid, int r)
{
T aux[r-l+1];
for(int i = l; i <= r; i++)
aux[i-l] = a[i];
int i = l;
int j = mid + 1;
for(int k = l; k <= r; k++)
{
if(i > mid)
{
a[k] = aux[j-l];
j++;
}
else if(j > r)
{
a[k] = aux[i-l];
i++;
}
else if(aux[i-l] < aux[j-l])
{
a[k] = aux[i-l];
i++;
}
else
{
a[k] = aux[j-l];
j++;
}
}
return;
}
template<typename T>
void __mergeSort(T a[], int l, int r)
{
//对于剩余小规模数组,比如剩下15时, 可以使用插入排序进行优化
if(l >= r)
return;
int mid = (l + r) / 2;
__mergeSort(a, l, mid);
__mergeSort(a, mid+1, r);
// 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
// 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
if( a[mid] > a[mid+1] )
__merge(a, l, mid, r);
return;
}
template<typename T>
void mergeSort(T a[], int n)
{
__mergeSort(a, 0, n-1);
return;
}

