快速排序

发表于 | 分类于 | | 浏览 次
字数统计: 3,721 字 | 阅读时长 ≈ 19 分钟

本文主要回顾快速排序，主要有如下内容：

  1. 白话快速排序
  2. 快速排序的具体实现
  3. 快速排序的问题与优化（两路快速排序与三路快速排序）

白话快速排序

快速排序被列为20世纪最伟大的算法之一，当然是因为其排序的效率高，但是其实算法也是在逐渐优化改进的。快速排序同归并排序一样，也采用分而治之的策略，但是分的策略是有差异的，后面准备专门写一篇来讲述分而治之，先说快速排序，其基本思想如下：

  1. 先从数列中取出一个数作为基准数。
  2. 分区过程，将比这个数大的或者等于它的数全放到它的右边，小于它的数全放到它的左边。
  3. 再对左右区间重复第二步，直到各区间只有一个数。


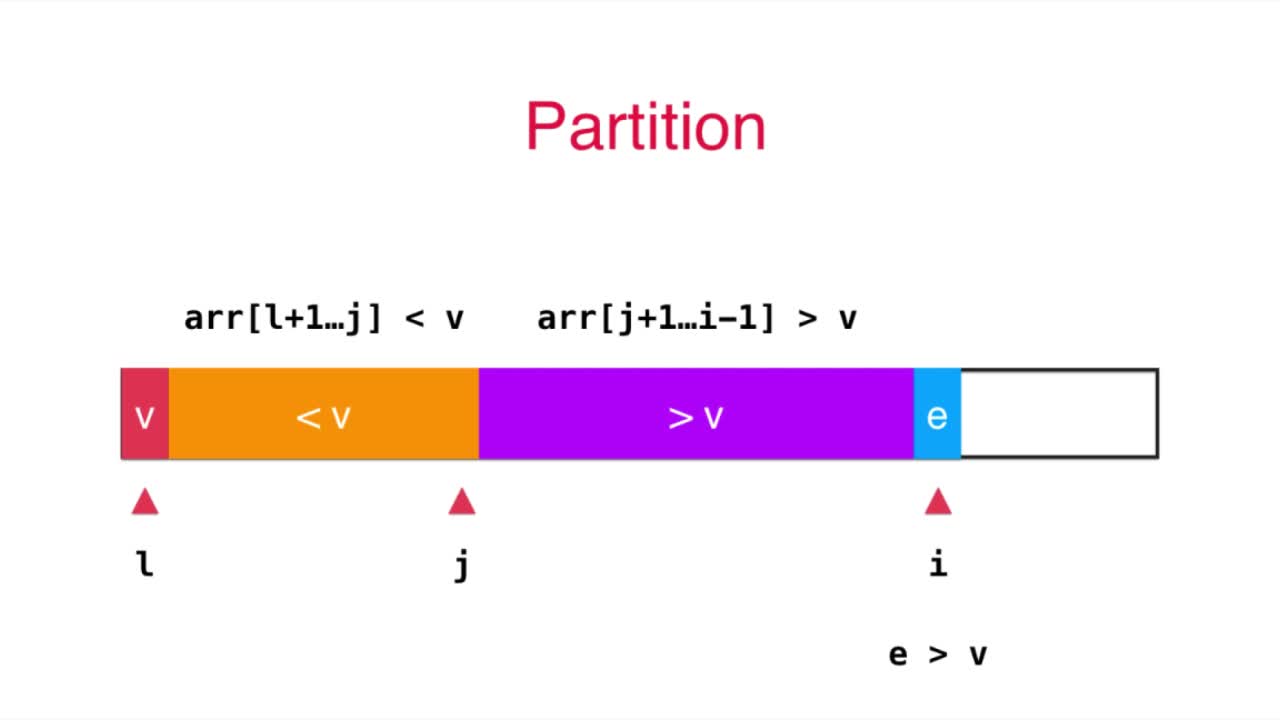
如上图，划分的过程中会出现如上图的情况，l+1到j的数都小于v（即图中橙色部分）,j+1到i（不包括i，i是当前正在考察的元素，考察完之后再决定加入哪个部分，即图中紫色部分，图中紫色）>=v，当前元素e如果小于v，那么需要将该元素放大橙色的部分，如何放呢？
就是将j后面一个元素与e所在元素交换，然后j计数加一即可。如果e不小于v，那直接放入紫色部分，i++即可。

快速排序通常情况下的时间复杂度为O( Nlog^N ),但是在某些特殊场景的下，比如完全有序的序列，会退化成O( N^2 )的时间复杂度，针对此种情况本文后面有优化方案，详见后文。

快速排序的具体实现

清单1 基本的快速排序实现–quickSort.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#ifndef QUICK_SORT_H
#define QUICK_SORT_H
#include <algorithm>

using namespace std;

template<typename T>
int __partitionQ(T a[], int l, int r)
{
    T e = a[l];
    //[l+1,j] < e;[j+1,i) > e
    int j = l;
    for(int i = l + 1; i <= r; i++)
    {
        if(a[i] < e)
        {
            j++;
            swap(a[j], a[i]);
        }
    }
    swap(a[l], a[j]);

    return j;
}

template<typename T>
void __quickSort(T a[], int l, int r)
{
    if(l >= r)
        return;

    int p = __partitionQ(a, l, r);
    __quickSort(a, l, p-1);
    __quickSort(a, p+1, r);


    return;
}

template<typename T>
void quickSort(T a[], int n)
{
    __quickSort(a, 0, n-1);

    return;
}
#endif // QUICK_SORT_H


清单2 main函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include "SortTestHelper.h"
//#include "selectionSort.h"
//#include "insertionSort.h"
//#include "shellSort.h"
#include "mergeSort.h"
#include "quickSort.h"

using namespace std;

int main()
{
    int n = 200000;
    cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
    int *arr = SortTestHelper::generateRandomArray(n, 0, n);
    int *arr1 = SortTestHelper::copyArray(arr, n);
    int *arr2 = SortTestHelper::copyArray(arr, n);
    int *arr3 = SortTestHelper::copyArray(arr, n);
    int *arr4 = SortTestHelper::copyArray(arr, n);
//    SortTestHelper::testSort("select Sort", selectionSort, arr, n);
//    //SortTestHelper::printArray(arr, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
//    //SortTestHelper::printArray(arr1, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr2, n);
//    //SortTestHelper::printArray(arr, n);
//
    SortTestHelper::testSort("Merge Sort", mergeSort, arr3, n);
//    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr4, n);
//    //SortTestHelper::printArray(arr4, n);
    delete[] arr;
    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;

    n=75000;
    int swaptime=100;
    cout<<"Test for nearly ordered array,size:"<<n<<", swap time = "<<swaptime<<"."<<endl;
    int *arr_n1 = SortTestHelper::generateNearlySortedArray(n, swaptime);
    int *arr_n2 = SortTestHelper::copyArray(arr_n1, n);

    SortTestHelper::testSort("Merge Sort", mergeSort, arr_n1, n);
    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr_n2, n);
    //SortTestHelper::printArray(arr4, n);

    delete[] arr_n1;
    delete[] arr_n2;

//    n=100000;
//    cout<<"Test for random array,size£º"<<n<<" range [0, "<<n<<"]."<<endl;
//    arr = SortTestHelper::generateRandomArray(n, 0, n);
//    arr1 = SortTestHelper::copyArray(arr, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr, n);
//    //SortTestHelper::printArray(arr, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
//    delete[] arr;
//    delete[] arr1;

    return 0;
}

注意：SortTestHelper.h与插入排序中清单1头文件相同。

清单3 上述程序运行结果（windows 10 笔记本，4G内存）

1
2
3
4
5
6
7
8
9
Test for random array,size:200000 range [0, 200000].
Merge Sort : 0.049 s
Quick sort : 0.034 s
Test for nearly ordered array,size:75000, swap time = 100.
Merge Sort : 0.013 s
Quick sort : 2.35 s

Process returned 0 (0x0)   execution time : 3.228 s
Press any key to continue.

快速排序的问题与优化

注意上面清单3的程序的运行结果：在随机的数组无序情况下，快速排序比归并排序稍微快一点，但差距不大；但是在近乎有序的情况，快速的运行时间为2.35秒，而同为O( Nlog^N )归并排序仅花了0.013s，快速排序比归并排序慢了180倍！！！这是为什么呢？？

原因是在近乎有序的情况下，上述的基本的快速排序实现的时间复杂度退化成了几乎是O( N^2 )

优化方法：基本的快速排序实现，在选取那个基准数的时候，每次都是选第一个，在有序的时候复杂度就退化成了O( N^2 )，在分而治之的时候，左边没有分到元素，全部都分到右边去了，左右两边极度的不平衡，因此优化方案就是避免此种情况出现，所以每次都随机选择一个基准数。

清单4 优化选择基准数后的快速排序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#ifndef QUICK_SORT_H
#define QUICK_SORT_H
#include <algorithm>
#include <ctime>

using namespace std;

template<typename T>
int __partitionQ(T a[], int l, int r)
{
    swap(a[l], a[rand()%(r-l+1)+l]);
    T e = a[l];
    //[l+1,j] < e;[j+1,i) > e
    int j = l;
    for(int i = l + 1; i <= r; i++)
    {
        if(a[i] < e)
        {
            j++;
            swap(a[j], a[i]);
        }
    }
    swap(a[l], a[j]);

    return j;
}

template<typename T>
void __quickSort(T a[], int l, int r)
{
    if(l >= r)
        return;

    int p = __partitionQ(a, l, r);
    __quickSort(a, l, p-1);
    __quickSort(a, p+1, r);


    return;
}

template<typename T>
void quickSort(T a[], int n)
{
    srand(time(NULL));
    __quickSort(a, 0, n-1);

    return;
}
#endif // QUICK_SORT_H

清单5 优化后的运行结果

1
2
3
4
5
6
7
8
9
Test for random array,size:200000 range [0, 200000].
Merge Sort : 0.062 s
Quick sort : 0.047 s
Test for nearly ordered array,size:75000, swap time = 100.
Merge Sort : 0.016 s
Quick sort : 0.015 s

Process returned 0 (0x0)   execution time : 0.749 s
Press any key to continue.

可以看到优化之后，快速排序与归并排序所消耗的时间已经相差无几了。

对有大量相同元素的数组进行排序测试

清单6 测试存在包含大量相同元素的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include "SortTestHelper.h"
#include "selectionSort.h"
#include "insertionSort.h"
#include "shellSort.h"
#include "mergeSort.h"
#include "quickSort.h"

using namespace std;

int main()
{
    int n = 200000;
    cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
    int *arr = SortTestHelper::generateRandomArray(n, 0, n);
    int *arr1 = SortTestHelper::copyArray(arr, n);
    int *arr2 = SortTestHelper::copyArray(arr, n);
    int *arr3 = SortTestHelper::copyArray(arr, n);
    int *arr4 = SortTestHelper::copyArray(arr, n);
//    SortTestHelper::testSort("select Sort", selectionSort, arr, n);
//    //SortTestHelper::printArray(arr, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
//    //SortTestHelper::printArray(arr1, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr2, n);
//    //SortTestHelper::printArray(arr, n);
//
    SortTestHelper::testSort("Merge Sort", mergeSort, arr3, n);
//    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr4, n);
//    //SortTestHelper::printArray(arr4, n);
    delete[] arr;
    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;

    n=200000;
    int swaptime=100;
    cout<<"Test for nearly ordered array,size:"<<n<<", swap time = "<<swaptime<<"."<<endl;
    int *arr_n1 = SortTestHelper::generateNearlySortedArray(n, swaptime);
    int *arr_n2 = SortTestHelper::copyArray(arr_n1, n);

    SortTestHelper::testSort("Merge Sort", mergeSort, arr_n1, n);
    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr_n2, n);
    //SortTestHelper::printArray(arr4, n);

    delete[] arr_n1;
    delete[] arr_n2;

    // 测试3 测试存在包含大量相同元素的数组
    // 使用双快速排序后, 我们的快速排序算法可以轻松的处理包含大量元素的数组
    cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
    arr1 = SortTestHelper::generateRandomArray(n,0,10);
    arr2 = SortTestHelper::copyArray(arr1, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
    SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);

    delete[] arr1;
    delete[] arr2;

//    n=100000;
//    cout<<"Test for random array,size£º"<<n<<" range [0, "<<n<<"]."<<endl;
//    arr = SortTestHelper::generateRandomArray(n, 0, n);
//    arr1 = SortTestHelper::copyArray(arr, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr, n);
//    //SortTestHelper::printArray(arr, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr1, n);
//    delete[] arr;
//    delete[] arr1;

    return 0;
}

测试结果
Test for random array,size:200000 range [0, 200000].
Merge Sort : 0.053 s
Quick sort : 0.031 s
Test for nearly ordered array,size:200000, swap time = 100.
Merge Sort : 0.024 s
Quick sort : 0.018 s
Test for random array, size = 200000, random range [0,10]
Merge Sort : 0.031 s
Quick Sort : 4.616 s

第三组测试，200000个数据在[0,10]之间，必然包含大量重复元素，此时发现快速排序比归并排序慢了148倍！！

####两路快速排序算法

在有很多重复元素的情况下，也会使得递归的过程变得很不平衡，很容易出现如下图的情况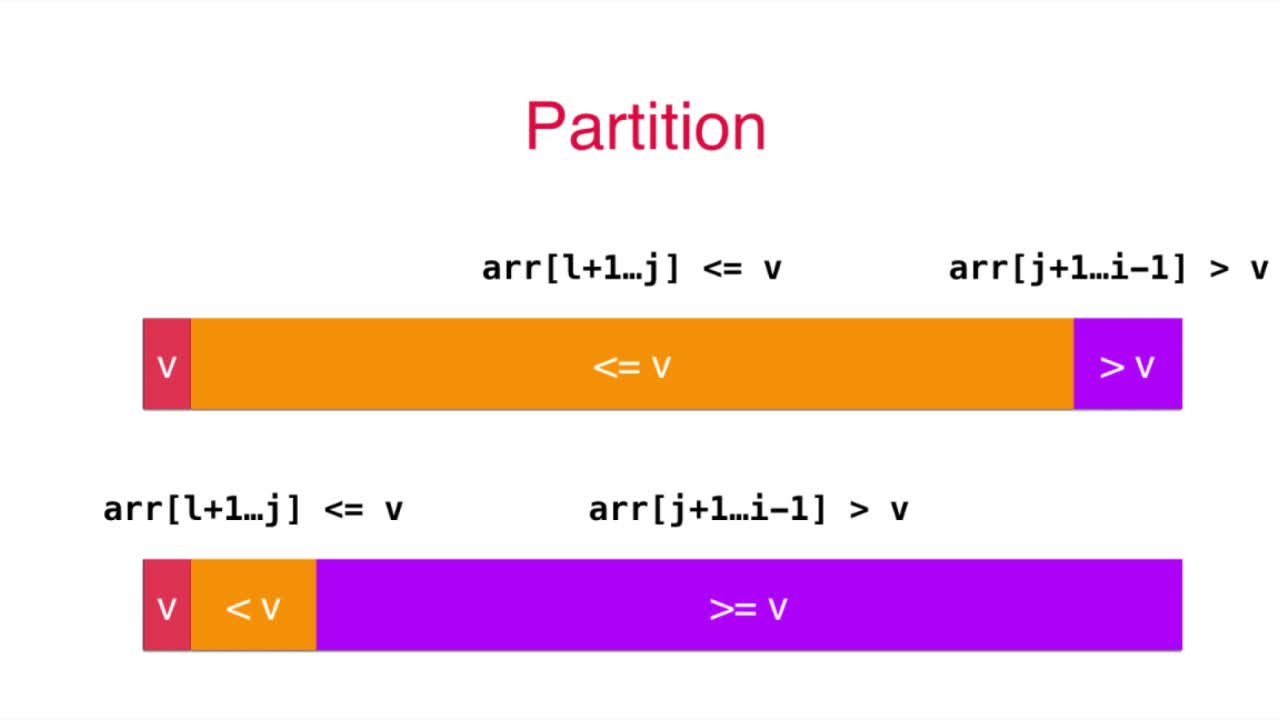

解决这种问题一个办法是采用双路快速排序，就是从数组的左右两边分别往中间的靠

双路快速排序示意图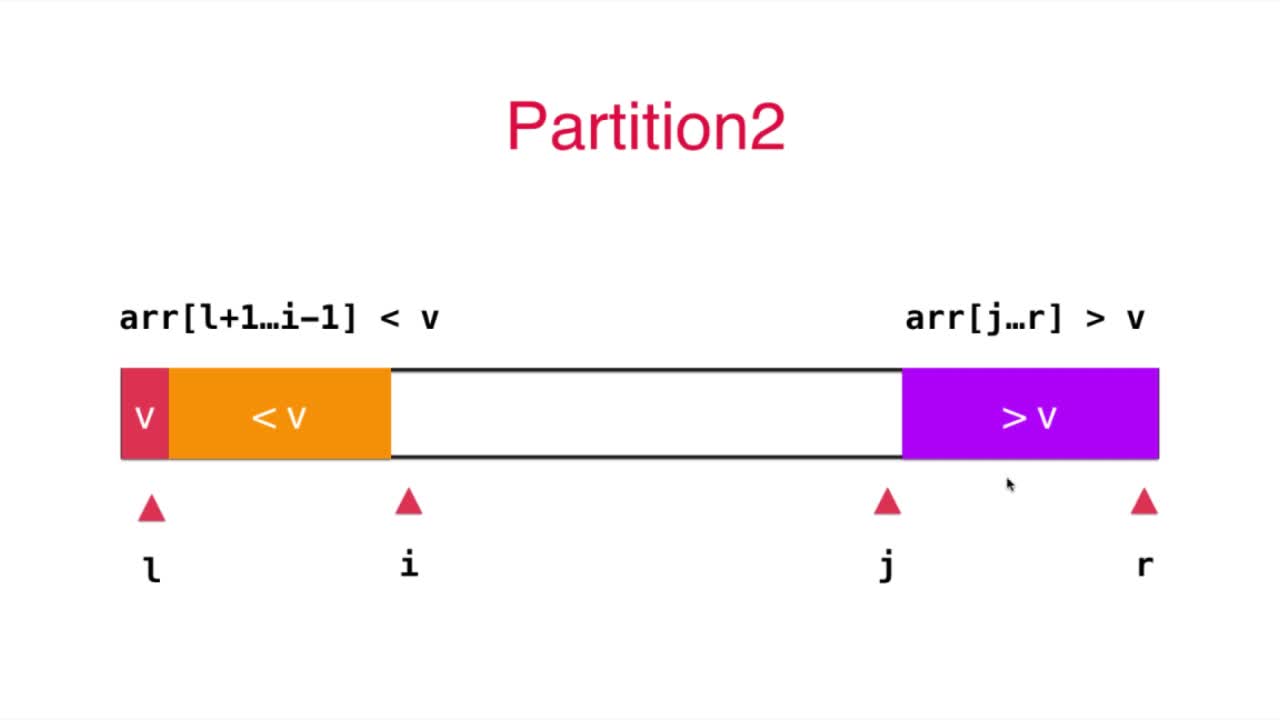

清单7 双路快速排序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#ifndef QUICK_SORT_H
#define QUICK_SORT_H
#include <algorithm>
#include <ctime>

using namespace std;

template<typename T>
int __partitionQ(T a[], int l, int r)
{
    swap(a[l], a[rand()%(r-l+1)+l]);
    T e = a[l];
    //[l+1,j] < e;[j+1,i) > e
//    int j = l;
//    for(int i = l + 1; i <= r; i++)
//    {
//        if(a[i] < e)
//        {
//            j++;
//            swap(a[j], a[i]);
//        }
//    }
//    swap(a[l], a[j]);
    //[l+1,i) < e; (j, r] > e
    int i = l + 1;
    int j = r;
    while(true)
    {
        while(i <= r && a[i] < e)
        {
            i++;
        }
        while(j >= l+1 && a[j] > e)
        {
            j--;
        }
        if(i > j)
            break;

        swap(a[i], a[j]);
        i++;
        j--;
    }

    swap(a[l], a[j]);

    return j;
}

template<typename T>
void __quickSort(T a[], int l, int r)
{
    if(l >= r)
        return;

    int p = __partitionQ(a, l, r);
    __quickSort(a, l, p-1);
    __quickSort(a, p+1, r);


    return;
}

template<typename T>
void quickSort(T a[], int n)
{
    srand(time(NULL));
    __quickSort(a, 0, n-1);

    return;
}
#endif // QUICK_SORT_H

三路快速排序算法

此外针对有大量重复元素的序列，还有一种三路快速排序算法，
基本思路是：
将arr分为三部分，分别为 arr[l+1… lt] < v, arr[lt+1… i-1] ==v, arr[gt…r] > v三部分，i指向待排元素(e)的位置
(1)当i<v时 swap(arr[lt+1], arr[i]) i++, lt++
(2)当i>v时 swap(arr[gt-1], arr[i]) gt–
(3)当e==v时i++

示意图如下：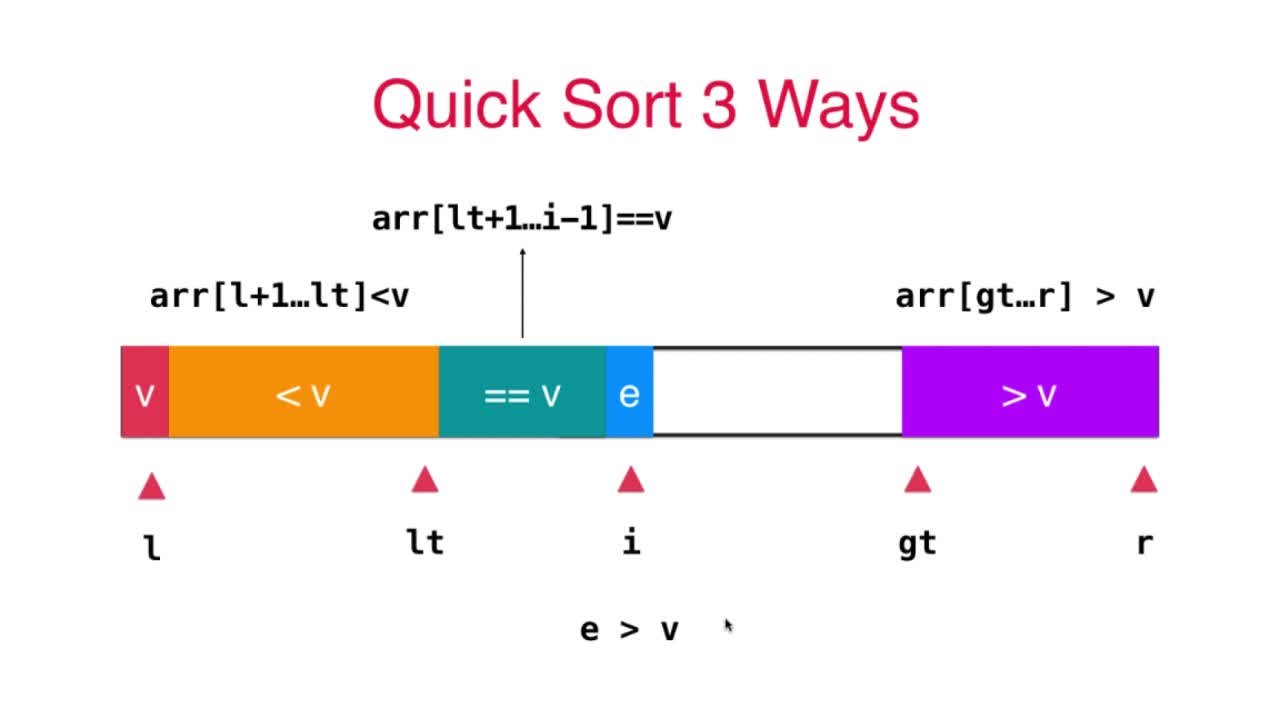

排序后：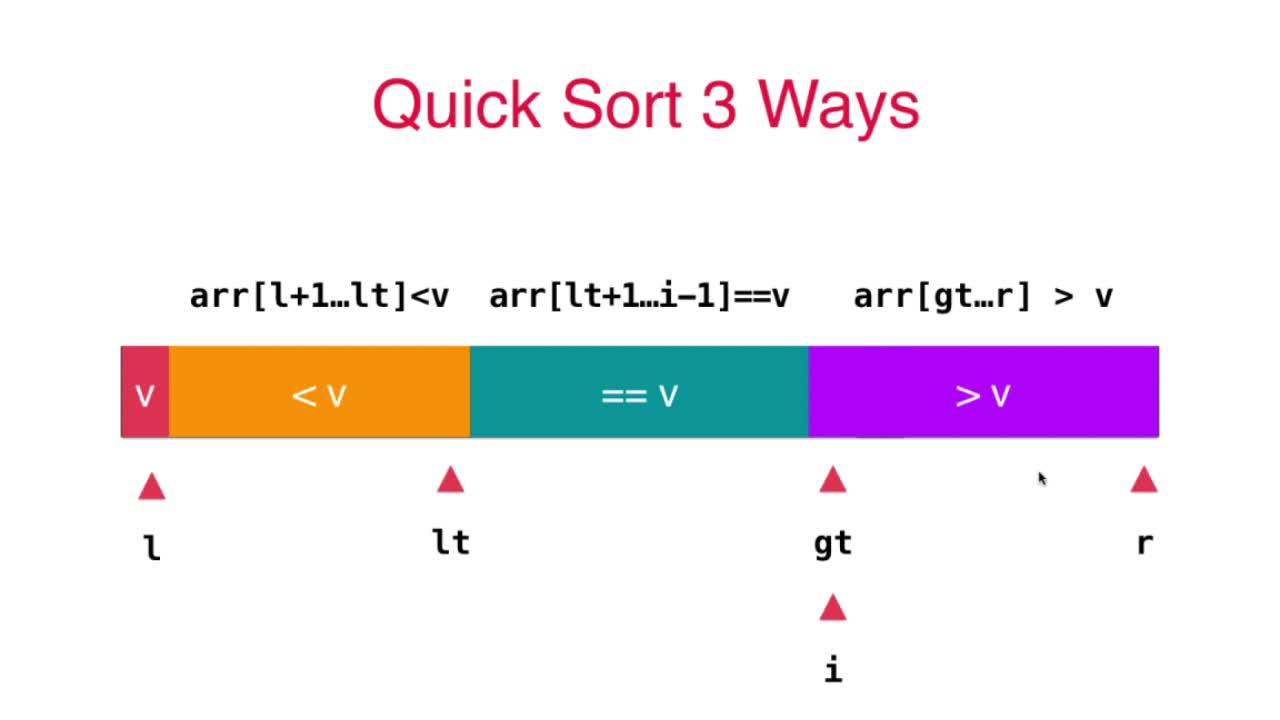

注意需要将v与arr[lt]交换，将v换到中间等于v的区域

三路快速排序的好处是如果有大量的重复元素，可以对这些处于中间重复元素不再进行处理，只需要处理两边区域里面的元素即可，可以节约时间

清单8 三路快速排序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#ifndef QUICK_SORT_H
#define QUICK_SORT_H

#include <ctime>

using namespace std;

//3路快速排序
//[l+1， lt] < e
//[gt, r] > e
//[lt+1, i) == e
template<typename T>
void __quickSort3Ways(T a[], int l, int r)
{
    if(l >= r)
    {
        return;
    }
    swap(a[l], a[rand()%(r-l+1)+l]);
    T v = a[l];

    int lt = l;
    int gt = r + 1;
    int i = l + 1;
    while(i < gt)
    {
        if(a[i] < v)
        {
            swap(a[i], a[lt+1]);
            lt++;
            i++;
        }
        else if(a[i] > v)
        {
            swap(a[i], a[gt-1]);
            gt--;
        }
        else
        {
            i++;
        }
    }
    swap(a[l], a[lt]);
    __quickSort3Ways(a, l, lt-1);
    __quickSort3Ways(a, gt, r);

    return;
}

template<typename T>
void quickSort3Ways(T a[], int n)
{
    srand(time(NULL));
    __quickSort3Ways(a, 0, n-1);

    return;
}

#endif // QUICK_SORT_H

清单9 测试函数main

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include "SortTestHelper.h"
#include "quickSort.h"

using namespace std;

int main()
{
    int n = 300000;
    cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
    int *arr = SortTestHelper::generateRandomArray(n, 0, n);
    int *arr1 = SortTestHelper::copyArray(arr, n);
    int *arr2 = SortTestHelper::copyArray(arr, n);
    int *arr3 = SortTestHelper::copyArray(arr, n);
    int *arr4 = SortTestHelper::copyArray(arr, n);

    SortTestHelper::testSort("Merge Sort", mergeSort, arr3, n);
//    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr4, n);
//    //SortTestHelper::printArray(arr4, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr, n);
    delete[] arr;
    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;

    n=300000;
    int swaptime=100;
    cout<<"Test for nearly ordered array,size:"<<n<<", swap time = "<<swaptime<<"."<<endl;
    int *arr_n1 = SortTestHelper::generateNearlySortedArray(n, swaptime);
    int *arr_n2 = SortTestHelper::copyArray(arr_n1, n);
    arr3 = SortTestHelper::copyArray(arr_n1, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr_n1, n);
    //SortTestHelper::printArray(arr3, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr_n2, n);
    //SortTestHelper::printArray(arr4, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr3, n);

    delete[] arr_n1;
    delete[] arr_n2;
    delete[] arr3;

    // 测试3 测试存在包含大量相同元素的数组
    // 使用双快速排序后, 我们的快速排序算法可以轻松的处理包含大量元素的数组
    cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
    arr1 = SortTestHelper::generateRandomArray(n,0,10);
    arr2 = SortTestHelper::copyArray(arr1, n);
    arr3 = SortTestHelper::copyArray(arr1, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr1, n);
    SortTestHelper::testSort("Quick Sort", quickSort, arr2, n);
    SortTestHelper::testSort("Quick Sort 3 ways", quickSort3Ways, arr2, n);

    delete[] arr1;
    delete[] arr2;
    delete[] arr3;


    return 0;
}

测试结果：

Test for random array,size:300000 range [0, 300000].
Merge Sort : 0.098 s
Quick sort : 0.066 s
Quick sort 3 ways : 0.057 s
Test for nearly ordered array,size:300000, swap time = 100.
Merge Sort : 0.042 s
Quick sort : 0.031 s
Quick sort 3 ways : 0.064 s
Test for random array, size = 300000, random range [0,10]
Merge Sort : 0.052 s
Quick Sort : 0.032 s
Quick Sort 3 ways : 0.011 s

从上述结果中可以看到，有大量重复元素时，三路快速排序的性能是很棒的

另外一个优化点，是在递归退出的时候，比如只剩下少量元素时选用插入排序，因为元素很少时，插入排序的性能是很棒的，所以插入排序经常用来优化归并排序和快速排序

清单10 用插入排序优化快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#ifndef QUICK_SORT_H
#define QUICK_SORT_H

#include <ctime>
#include "insertionSort.h"

using namespace std;

//双路快速排序的partition函数
template<typename T>
int __partitionQ2(T a[], int l, int r)
{
    swap(a[l], a[rand()%(r-l+1)+l]);
    T v = a[l];
    //[l+1, i) < v (j, r] > v
    int i = l + 1;
    int j = r;
    while(true)
    {
        while(i <= r && a[i] < v)
        {
            i++;
        }
        while(j >= l + 1 && a[j] > v)
        {
            j--;
        }

        if(i > j)
        {
            break;
        }

        swap(a[i], a[j]);
        i++;
        j--;
    }

    swap(a[l], a[j]);

    return j;
}

template<typename T>
void __quickSort(T a[], int l, int r)
{
    //利用插入排序优化快速排序
    if(r - l <= 15)
    {
        insertionSort(a, l, r);
        return;
    }

    int p = __partitionQ2(a, l, r);
    __quickSort(a, l, p-1);
    __quickSort(a, p+1, r);

    return;
}


template<typename T>
void quickSort(T a[], int n)
{
    srand(time(NULL));
    __quickSort(a, 0, n-1);

    return;
}

#endif // QUICK_SORT_H

对于 insertionSort(a, l, r)这样子的插入排序本文就省略了，可以参考插入排序一文自己实现。

参考资料

[算法（第4版）]

如果你觉得本文对你有帮助，欢迎打赏