堆排序

发表于 | 分类于 | | 浏览 次
字数统计: 4,524 字 | 阅读时长 ≈ 23 分钟

本文主要回顾堆排序，主要有如下内容：

  1. 优先级队列
  2. 堆及堆的基本实现
  3. 堆排序的实现及优化

优先级队列

普通队列：先进先出，后进后出；
优先级队列：出队顺序与入队顺序无关，和优先级有关。比如绝大多数手机分配给来电的优先级都会比游戏程序的高。
一种合适数据结构应该支持两种操作：删除最大元素（取出优先级最高的元素）和插入元素，这种数据类型叫做优先级队列。

优先级队列的实现

优先级队列的具体实现可以用普通数组、顺序数组，还可以用堆，如下图所示：

可以看到对于总共N个请求：

  • 使用普通数组或者顺序数组，最差情况时间复杂度为：O( n^2 )
  • 使用堆:O(nlogn)

优先队列的应用场景

  • 操作系统的任务调度处理（根据任务优先级进行调度）
  • 游戏AI自动攻击在范围内的敌人（比如范围内敌人很多，便可根据优先级队列进行选择:) ）
  • 堆排序
    ….

堆是优先级队列的一种经典实现方法，准确的说，二叉堆是优先级队列的一种经典实现方法，当然也可以用d-叉堆来实现（比如三叉堆）。

堆及其基本实现

堆是一种数据结构，其经典实现是二叉堆，二叉堆可以视为一棵完全二叉树，关于完全二叉树请参考这篇文章。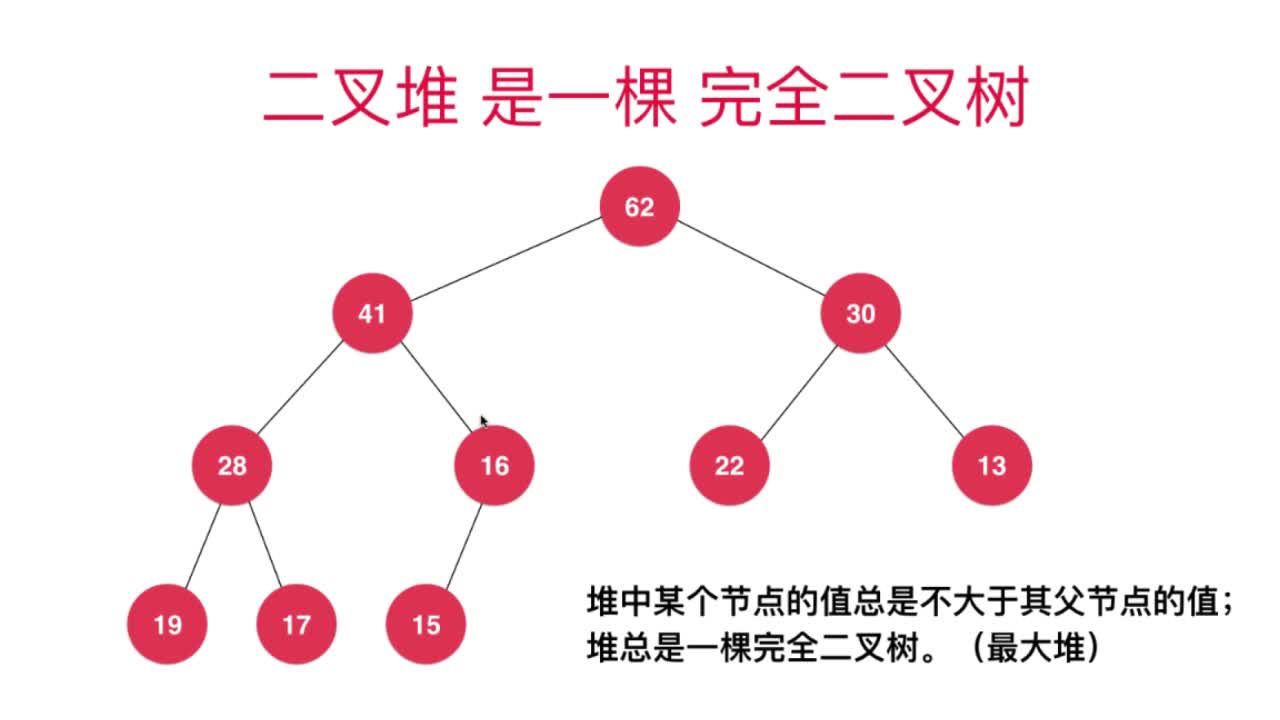

二叉堆的表示法
既然二叉堆是一颗完全二叉树，我们很自然的想到了用指针来构造二叉堆；
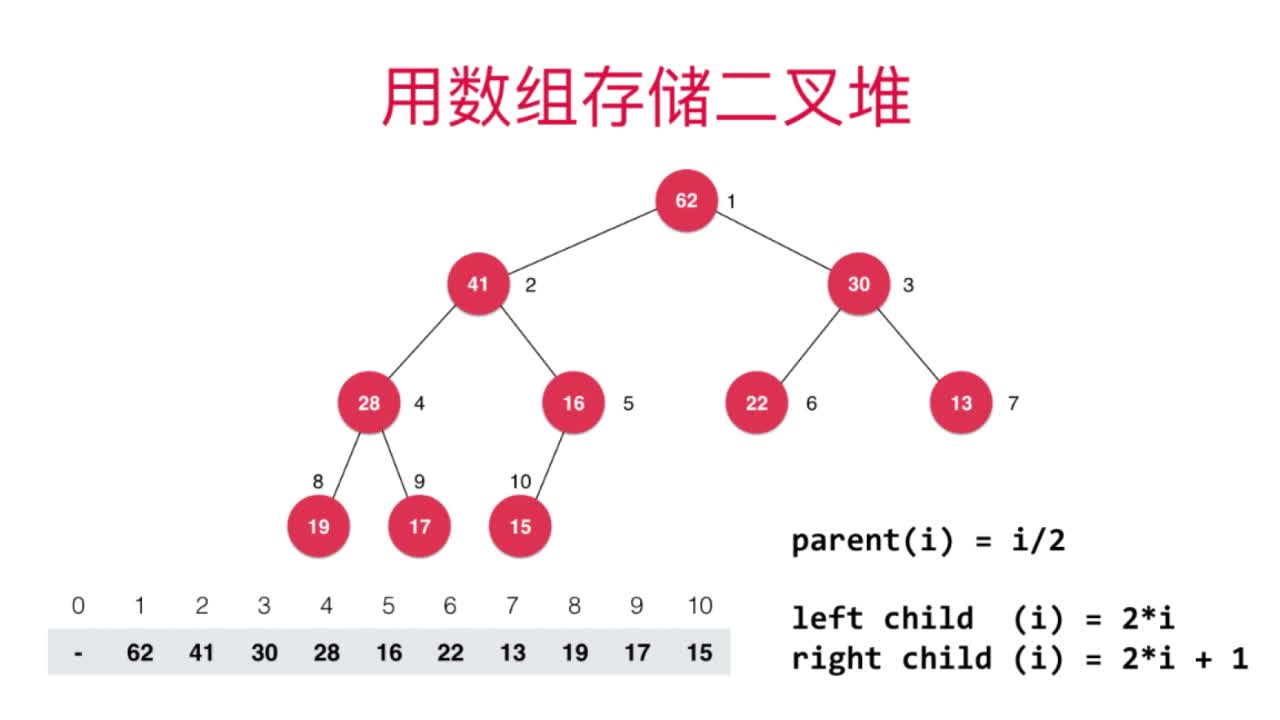
不过还可以使用数组的索引来表示元素在二叉堆中的位置，如下图：

这是二叉堆的一种经典表示法，不使用数组的第一个位置即a[0],那么容易看出：

  • 元素k的父节点所在的位置为[i/2]（向下取整，比如5/2向下取整得2）
  • 元素k的子节点所在的位置为2i和2i+1

堆有最大堆（有的叫“大顶堆”）最小堆（有的叫“小顶堆”），二者可以用如下公式进行定义：

  • 最大堆：arr[k] >= arr[2k] && arr[k] >= arr[2k+1]
  • 最小堆：arr[k] <= arr[2k] && arr[k] <= arr[2k+1]

本文在后面实现堆排序时，采用最大堆。

堆的基本实现

清单1 堆的基本实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#ifndef HEAP_H
#define HEAP_H
#include <cassert>

using namespace std;

template<typename Item>
class MaxHeap
{
private:
    Item* data;
    int count;
    int capacity;

public:
    MaxHeap(int capacity)
    {
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    ~MaxHeap()
    {
        delete[] data;
    }

    int size()
    {
        return count;
    }

    bool isEmpty()
    {
        return count == 0;
    }

};

#endif // HEAP_H

堆排序及其基本实现

了解了前面的相关知识后，可以介绍堆排序了，其实就是用来最大堆的特性。
堆排序基本思想是:
将待排序序列构造成一个最大堆，此时，整个序列的最大值就是堆顶的根节点，取出根节点后，剩下元素重新构造形成一个最大堆，再取出根节点…如此反复，便能得到一个有序序列了（需要注意这样得到的序列是从大到小的）。

堆排序的基本实现

清单2 堆的基本操作实现heap.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#ifndef HEAP_H
#define HEAP_H
#include <cassert>

using namespace std;

template<typename Item>
class MaxHeap
{
private:
    Item* data;
    int count;
    int capacity;

    void shiftUp(int k)
    {
        while(k > 1 && data[k/2] < data[k])
        {
            swap(data[k/2], data[k]);
            k /= 2;
        }
    }

    void shiftDown(int k)
    {
        while(2*k <= count)
        {
            int j = 2*k;
            if(j+1 <= count && data[j+1] > data[j])
            {
                j++;
            }
            if(data[k] >= data[j])
            {
                break;
            }
            swap(data[k], data[j]);
            k = j;
        }
    }

public:
    MaxHeap(int capacity)
    {
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }
    
    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    MaxHeap(Item arr[], int n)
    {
        data = new Item[n+1];
        capacity = n;
        for(int i = 0; i < n; i++)
        {
            data[i+1] = arr[i];
        }
        count = n;

        for(int i = count/2; i >= 1; i--)
        {
            shiftDown(i);
        }
    }

    ~MaxHeap()
    {
        delete[] data;
    }

    int size()
    {
        return count;
    }

    bool isEmpty()
    {
        return count == 0;
    }

    void insert(Item item)
    {
        assert(count+1 <= capacity);
        data[count+1] = item;
        shiftUp(count+1);
        count++;
    }

    Item extractMax()
    {
        Item ret = data[1];
        swap(data[1], data[count]);
        count--;
        shiftDown(1);

        return ret;
    }
};

#endif // HEAP_H


清单3 堆排序基本实现heapSort.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#ifndef HEAP_SORT_H
#define HEAP_SORT_H

#include "heap.h"

using namespace std;

// heapSort1, 将所有的元素依次添加到堆中, 在将所有元素从堆中依次取出来, 即完成了排序
// 无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn)
// 整个堆排序的整体时间复杂度为O(nlogn)
template<typename T>
void heapSort1(T arr[], int n)
{
    MaxHeap<T> maxheap = MaxHeap<T>(n);

    for(int i = 0; i < n; i++)
    {
        maxheap.insert(arr[i]);
    }

    for(int i = n-1; i >= 0; i--)
    {
        arr[i] = maxheap.extractMax();
    }

    return;
}

#endif // HEAP_SORT_H

堆排序优化一

heapSort1, 将所有的元素依次添加到堆中, 在将所有元素从堆中依次取出来, 即完成了排序,无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn); 整个堆排序的整体时间复杂度为O(nlogn)。

另一种办法是将数组直接先构造成一个最大堆，然后再从堆中依次取出元素。构造一个最大堆的过程被称为heapify

heapify的代码见清单2中“通过一个给定数组创建一个最大堆的构造函数”
直接通过数组的方式构造堆，其复杂度为O(n);将n个元素逐个插入空堆中来构造堆，复杂度是O(nlogn)

清单4 加入优化heapSort2的heapSort.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#ifndef HEAP_SORT_H
#define HEAP_SORT_H

#include "heap.h"

using namespace std;
template<typename T>
void heapSort1(T arr[], int n)
{
    MaxHeap<T> maxheap = MaxHeap<T>(n);

    for(int i = 0; i < n; i++)
    {
        maxheap.insert(arr[i]);
    }

    for(int i = n-1; i >= 0; i--)
    {
        arr[i] = maxheap.extractMax();
    }

    return;
}

template<typename T>
void heapSort2(T arr[], int n)
{
    MaxHeap<T> maxheap = MaxHeap<T>(arr, n);

    for(int i = n-1; i >= 0; i--)
    {
        arr[i] = maxheap.extractMax();
    }
}

#endif // HEAP_SORT_H

清单5 测试程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <iostream>
#include "SortTestHelper.h"
//#include "selectionSort.h"
#include "insertionSort.h"
#include "shellSort.h"
//#include "bubbleSort.h"
#include "mergeSort.h"
#include "quickSort.h"
#include "heapSort.h"

using namespace std;

int main()
{
    int n = 100000;
    cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
    int *arr1 = SortTestHelper::generateRandomArray(n, 0, n);
    int *arr2 = SortTestHelper::copyArray(arr1, n);
    int *arr3 = SortTestHelper::copyArray(arr1, n);
    int *arr4 = SortTestHelper::copyArray(arr1, n);
    int *arr5 = SortTestHelper::copyArray(arr1, n);
    int *arr6 = SortTestHelper::copyArray(arr1, n);
    int *arr7 = SortTestHelper::copyArray(arr1, n);
    int *arr8 = SortTestHelper::copyArray(arr1, n);
    int *arr9 = SortTestHelper::copyArray(arr1, n);
    int *arr10 = SortTestHelper::copyArray(arr1, n);
//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2 Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);
    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;

    // 测试2 近乎有序的数组
    n=100000;
    int swaptime=100;
    cout<<"Test for nearly ordered array,size:"<<n<<", swap time = "<<swaptime<<"."<<endl;
    arr1 = SortTestHelper::generateNearlySortedArray(n, swaptime);
    arr2 = SortTestHelper::copyArray(arr1, n);
    arr3 = SortTestHelper::copyArray(arr1, n);
    arr4 = SortTestHelper::copyArray(arr1, n);
    arr5 = SortTestHelper::copyArray(arr1, n);
    arr6 = SortTestHelper::copyArray(arr1, n);
    arr7 = SortTestHelper::copyArray(arr1, n);
    arr8 = SortTestHelper::copyArray(arr1, n);
    arr9 = SortTestHelper::copyArray(arr1, n);
    arr10 = SortTestHelper::copyArray(arr1, n);

//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);

    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;

    // 测试3 测试存在包含大量相同元素的数组
    // 使用双快速排序后, 我们的快速排序算法可以轻松的处理包含大量元素的数组
    cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
    arr1 = SortTestHelper::generateRandomArray(n,0,10);
    arr2 = SortTestHelper::copyArray(arr1, n);
    arr3 = SortTestHelper::copyArray(arr1, n);
    arr4 = SortTestHelper::copyArray(arr1, n);
    arr5 = SortTestHelper::copyArray(arr1, n);
    arr6 = SortTestHelper::copyArray(arr1, n);
    arr7 = SortTestHelper::copyArray(arr1, n);
    arr8 = SortTestHelper::copyArray(arr1, n);
    arr9 = SortTestHelper::copyArray(arr1, n);
    arr10 = SortTestHelper::copyArray(arr1, n);
//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);

    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;

    return 0;
}


注意测试程序中其他排序排序算法的具体实现请参考前面的文章。
运行结果：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Test for random array,size:100000 range [0, 100000].
Insert Sort : 7.344 s
Shell Sort : 0.02 s
Merge sort : 0.021 s
Quick sort : 0.018 s
Quick sort 2 Ways : 0.016 s
Quick sort 3 ways : 0.02 s
Heap sort 1 : 0.033 s
Heap sort 2 : 0.03 s
Test for nearly ordered array,size:100000, swap time = 100.
Insert Sort : 0.008 s
Shell Sort : 0.004 s
Merge Sort : 0.016 s
Quick sort : 0.012 s
Quick sort 2Ways : 0.008 s
Quick sort 3 ways : 0.021 s
Heap sort 1 : 0.034 s
Heap sort 2 : 0.02 s
Test for random array, size = 100000, random range [0,10]
Insert Sort : 6.6 s
Shell Sort : 0.008 s
Merge Sort : 0.016 s
Quick sort : 1.164 s
Quick sort 2Ways : 0.016 s
Quick sort 3 ways : 0.004 s
Heap sort 1 : 0.028 s
Heap sort 2 : 0.024 s

可以看到，进行优化后，heapSort2比heapSort1稍微快一点。

堆排序优化二
前面的两种方法都是用了额外的最大堆，因此可以直接在原数组上进行原地的堆排序。
优化之后的代码见清单6

堆排序优化方法三
堆排序shiftDown过程中有许多swap操作，可以像插入排序一样把swap操作优化掉。
注意在优化二和优化三中，直接使用了原地排序，也就使用了数组的第一个位置即a[0],那么容易看出：

  • 元素k的父节点所在的位置为[(i-1)/2]（向下取整，比如5/2向下取整得2）
  • 元素k的子节点所在的位置为2i+1和2i+2

清单6 加入原地堆排序的heapSort.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#ifndef HEAP_SORT_H
#define HEAP_SORT_H

#include "heap.h"

using namespace std;
template<typename T>
void heapSort1(T arr[], int n)
{
    MaxHeap<T> maxheap = MaxHeap<T>(n);

    for(int i = 0; i < n; i++)
    {
        maxheap.insert(arr[i]);
    }

    for(int i = n-1; i >= 0; i--)
    {
        arr[i] = maxheap.extractMax();
    }

    return;
}

template<typename T>
void heapSort2(T arr[], int n)
{
    MaxHeap<T> maxheap = MaxHeap<T>(arr, n);

    for(int i = n-1; i >= 0; i--)
    {
        arr[i] = maxheap.extractMax();
    }
}


// 原始的shiftDown过程
template<typename T>
void __shiftDown1(T arr[], int n, int k)
{

    while( 2*k+1 < n )
    {
        int j = 2*k+1;
        if( j+1 < n && arr[j+1] > arr[j] )
            j += 1;

        if( arr[k] >= arr[j] )break;

        swap( arr[k] , arr[j] );
        k = j;
    }
}

// 优化的shiftDown过程, 使用赋值的方式取代不断的swap,
// 该优化思想和我们之前对插入排序进行优化的思路是一致的
template<typename T>
void __shiftDown2(T arr[], int n, int k){

    T e = arr[k];
    while( 2*k+1 < n ){
        int j = 2*k+1;
        if( j+1 < n && arr[j+1] > arr[j] )
            j += 1;

        if( e >= arr[j] ) break;

        arr[k] = arr[j];
        k = j;
    }

    arr[k] = e;
}

// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort3(T arr[], int n)
{

    // 注意，此时我们的堆是从0开始索引的
    // 从(最后一个元素的索引-1)/2开始
    // 最后一个元素的索引 = n-1
    for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
        __shiftDown1(arr, n, i);

    for( int i = n-1; i > 0 ; i-- )
    {
        swap( arr[0] , arr[i] );
        __shiftDown1(arr, i, 0);
    }
}

// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort4(T arr[], int n)
{

    // 注意，此时我们的堆是从0开始索引的
    // 从(最后一个元素的索引-1)/2开始
    // 最后一个元素的索引 = n-1
    for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
        __shiftDown2(arr, n, i);

    for( int i = n-1; i > 0 ; i-- )
    {
        swap( arr[0] , arr[i] );
        __shiftDown2(arr, i, 0);
    }
}

#endif // HEAP_SORT_H


清单7 测试程序main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include <iostream>
#include "SortTestHelper.h"
//#include "selectionSort.h"
#include "insertionSort.h"
#include "shellSort.h"
//#include "bubbleSort.h"
#include "mergeSort.h"
#include "quickSort.h"
#include "heapSort.h"

using namespace std;

int main()
{
    int n = 400000;
    cout<<"Test for random array,size:"<<n<<" range [0, "<<n<<"]."<<endl;
    int *arr1 = SortTestHelper::generateRandomArray(n, 0, n);
    int *arr2 = SortTestHelper::copyArray(arr1, n);
    int *arr3 = SortTestHelper::copyArray(arr1, n);
    int *arr4 = SortTestHelper::copyArray(arr1, n);
    int *arr5 = SortTestHelper::copyArray(arr1, n);
    int *arr6 = SortTestHelper::copyArray(arr1, n);
    int *arr7 = SortTestHelper::copyArray(arr1, n);
    int *arr8 = SortTestHelper::copyArray(arr1, n);
    int *arr9 = SortTestHelper::copyArray(arr1, n);
    int *arr10 = SortTestHelper::copyArray(arr1, n);
    int *arr11 = SortTestHelper::copyArray(arr1, n);
    int *arr12 = SortTestHelper::copyArray(arr1, n);
//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2 Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);
    SortTestHelper::testSort("Heap sort 3", heapSort3, arr11, n);
    SortTestHelper::testSort("Heap sort 4", heapSort4, arr12, n);
    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;
    delete[] arr11;
    delete[] arr12;

    // 测试2 近乎有序的数组
    n=400000;
    int swaptime=100;
    cout<<"Test for nearly ordered array,size:"<<n<<", swap time = "<<swaptime<<"."<<endl;
    arr1 = SortTestHelper::generateNearlySortedArray(n, swaptime);
    arr2 = SortTestHelper::copyArray(arr1, n);
    arr3 = SortTestHelper::copyArray(arr1, n);
    arr4 = SortTestHelper::copyArray(arr1, n);
    arr5 = SortTestHelper::copyArray(arr1, n);
    arr6 = SortTestHelper::copyArray(arr1, n);
    arr7 = SortTestHelper::copyArray(arr1, n);
    arr8 = SortTestHelper::copyArray(arr1, n);
    arr9 = SortTestHelper::copyArray(arr1, n);
    arr10 = SortTestHelper::copyArray(arr1, n);
    arr11 = SortTestHelper::copyArray(arr1, n);
    arr12 = SortTestHelper::copyArray(arr1, n);

//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);
    SortTestHelper::testSort("Heap sort 3", heapSort3, arr11, n);
    SortTestHelper::testSort("Heap sort 4", heapSort4, arr12, n);

    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;
    delete[] arr11;
    delete[] arr12;

    // 测试3 测试存在包含大量相同元素的数组
    // 使用双快速排序后, 我们的快速排序算法可以轻松的处理包含大量元素的数组
    cout<<"Test for random array, size = "<<n<<", random range [0,10]"<<endl;
    arr1 = SortTestHelper::generateRandomArray(n,0,10);
    arr2 = SortTestHelper::copyArray(arr1, n);
    arr3 = SortTestHelper::copyArray(arr1, n);
    arr4 = SortTestHelper::copyArray(arr1, n);
    arr5 = SortTestHelper::copyArray(arr1, n);
    arr6 = SortTestHelper::copyArray(arr1, n);
    arr7 = SortTestHelper::copyArray(arr1, n);
    arr8 = SortTestHelper::copyArray(arr1, n);
    arr9 = SortTestHelper::copyArray(arr1, n);
    arr10 = SortTestHelper::copyArray(arr1, n);
    arr11 = SortTestHelper::copyArray(arr1, n);
    arr12 = SortTestHelper::copyArray(arr1, n);

//    SortTestHelper::testSort("select Sort", selectionSort, arr1, n);
//    SortTestHelper::testSort("Insert Sort", insertionSort, arr2, n);
//    SortTestHelper::testSort("Shell Sort", shellSort, arr3, n);
//    SortTestHelper::testSort("Bubble Sort", bubbleSort, arr4, n);
    SortTestHelper::testSort("Merge Sort", mergeSort, arr5, n);
    SortTestHelper::testSort("Quick sort", quickSort, arr6, n);
    SortTestHelper::testSort("Quick sort 2Ways", quickSort2Ways, arr7, n);
    SortTestHelper::testSort("Quick sort 3 ways", quickSort3Ways, arr8, n);
    SortTestHelper::testSort("Heap sort 1", heapSort1, arr9, n);
    SortTestHelper::testSort("Heap sort 2", heapSort2, arr10, n);
    SortTestHelper::testSort("Heap sort 3", heapSort3, arr11, n);
    SortTestHelper::testSort("Heap sort 4", heapSort4, arr12, n);

    delete[] arr1;
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;
    delete[] arr5;
    delete[] arr6;
    delete[] arr7;
    delete[] arr8;
    delete[] arr9;
    delete[] arr10;
    delete[] arr11;
    delete[] arr12;

    return 0;
}


运行结果：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Test for random array,size:400000 range [0, 400000].
Merge sort : 0.078 s
Quick sort : 0.079 s
Quick sort 2 Ways : 0.062 s
Quick sort 3 ways : 0.078 s
Heap sort 1 : 0.125 s
Heap sort 2 : 0.123 s
Heap sort 3 : 0.11 s
Heap sort 4 : 0.078 s
Test for nearly ordered array,size:400000, swap time = 100.
Merge Sort : 0.062 s
Quick sort : 0.047 s
Quick sort 2Ways : 0.047 s
Quick sort 3 ways : 0.094 s
Heap sort 1 : 0.125 s
Heap sort 2 : 0.093 s
Heap sort 3 : 0.078 s
Heap sort 4 : 0.063 s
Test for random array, size = 400000, random range [0,10]
Merge Sort : 0.062 s
Quick sort : 17.537 s
Quick sort 2Ways : 0.031 s
Quick sort 3 ways : 0.016 s
Heap sort 1 : 0.094 s
Heap sort 2 : 0.093 s
Heap sort 3 : 0.094 s
Heap sort 4 : 0.063 s

在N个元素中选出前M个元素，普通队列排序：NlogN;
优先队列：NlogM
堆排序主要用于动态数据的维护。

参考资料

[算法（第4版）]
完美二叉树, 完全二叉树和完满二叉树
经典算法和数据结构(一) 优先级队列与堆排序
图解排序算法(三)之堆排序

如果你觉得本文对你有帮助，欢迎打赏