二叉搜索树

发表于 | 分类于 | | 浏览 次
字数统计: 3,802 字 | 阅读时长 ≈ 17 分钟

二叉搜索树有的叫二分搜索树，还有的叫二叉查找树。
本文主要回顾二叉搜索树，主要有如下内容：

  1. 二叉搜索树的特点及优势
  2. 二叉搜索树的基本操作（插入、查找）
  3. 二叉搜索树的深度优先遍历（前序、中序、后序遍历）
  4. 二叉搜索树的广度优先遍历（层序遍历）
  5. 二叉搜索树删除操作（最小值、最大值、指定节点）
  6. 二叉搜索树的顺序性
  7. 二叉搜索树的局限性
  8. 总结

二叉搜索树的特点及优势

二叉搜索树本质是一棵二叉树，有如下特点：

  • 每个节点的键值大于左孩子
  • 每个节点的键值小于右孩子
  • 以左右孩子为根的子树仍为二叉搜索树

从其特点可以看出，二叉树天然带有递归的特点 ：)
注意前面的讲堆排序中的二叉堆是一个完全二叉树，但是二叉搜索树不一定是完全二叉树。

二叉搜索树的优势：

时间复杂度对比

不仅可查找数据，还可以高效地插入，删除数据之类的动态维护数据。
可以方便地回答很多数据之间的关系问题：
min, max
floor, ceil
rank
select

二叉搜索树的基本操作

二叉搜索树的插入操作

判断node节点是否为空，为空则创建节点并将其返回（ 判断递归到底的情况）。
若不为空，则继续判断根元素的key值是否等于根元素的key值：

  • 若相等则直接更新value值即可。
  • 若不相等，则根据其大小比较在左孩子或右孩子部分继续递归直至找到合适位置为止。

插入操作代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public:
    // 向二分搜索树中插入一个新的(key, value)数据对
    void insert(Key key, Value value)
    {
        root = insert(root, key, value);
    }

private:
    Node* insert(Node* node, Key key, Value value)
    {
        if(NULL == node)
        {
            count++;
            return new Node(key, value);
        }

        if(key == node->key)
        {
            node->value = value;
        }
        else if(key < node->key)
        {
            node->left = insert(node->left, key, value);
        }
        else
        {
            node->right = insert(node->right, key, value);
        }

        return node;
    }

二叉搜索树的查找操作

理解上面的插入操作之后，查找操作的过程本质是一样的，插入是找到合适的位置插入节点，查找是要找特定key的值。
这里直接给出 Value search(Key key)：在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL。（注意：这里返回值使用Value ，是为了避免用户查找的值并不存在而出现异常）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public:
    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL
    Value* search(Key key)
    {
        return search(root, key);
    }
    
private:
    Value* search(Node* node, Key key)
    {
        if(NULL == node)
        {
            return NULL;
        }

        if(key == node->key)
        {
            return &(node->value);
        }
        else if(key < node->key)
        {
            return search(node->left, key);
        }
        else
        {
            return search(node->right, key);
        }
    }

二叉搜索树的深度优先遍历

前序遍历：先访问当前节点，再依次递归访问左右子树
可以参考下图进行理解：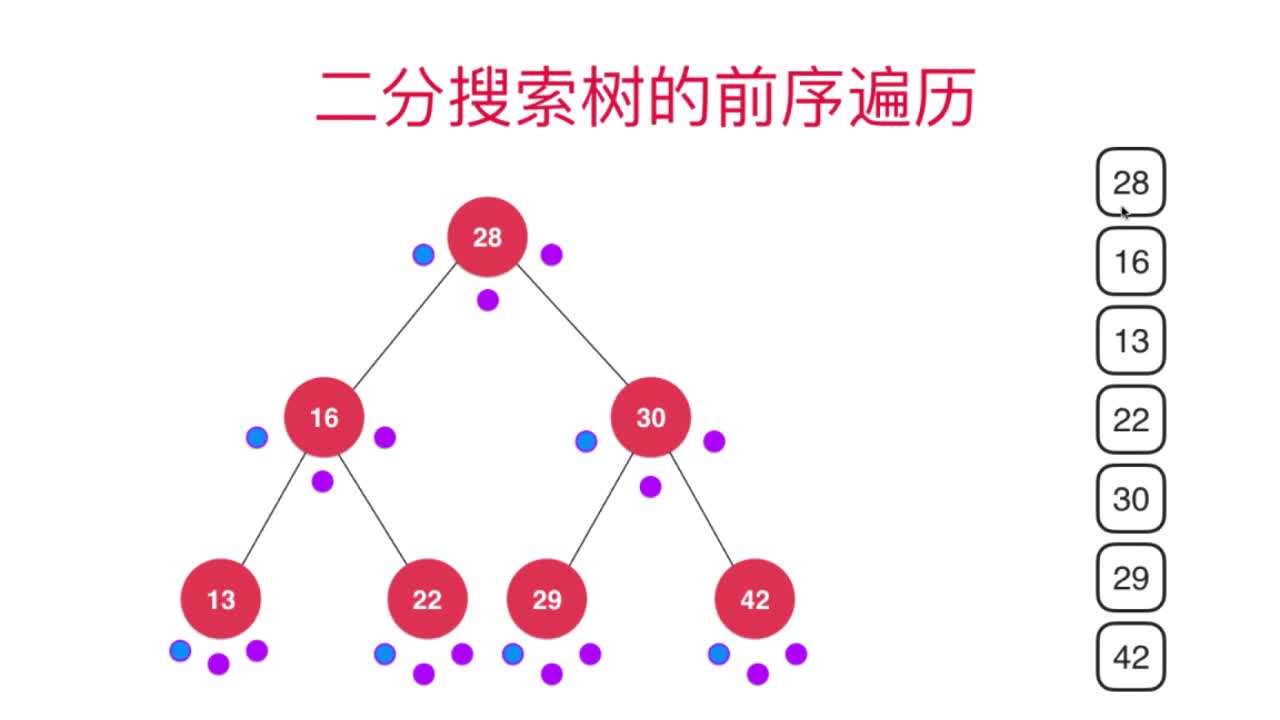

其实在遍历过程中每个节点都访问了3次，对应着这3个小点，顺序为前-> 中 -> 后，只有在“前”点时才会打印该节点元素值即上图中蓝色的点）。

中序遍历：先递归访问左子树，再访问自身，再递归访问右子树
可以参考下图进行理解：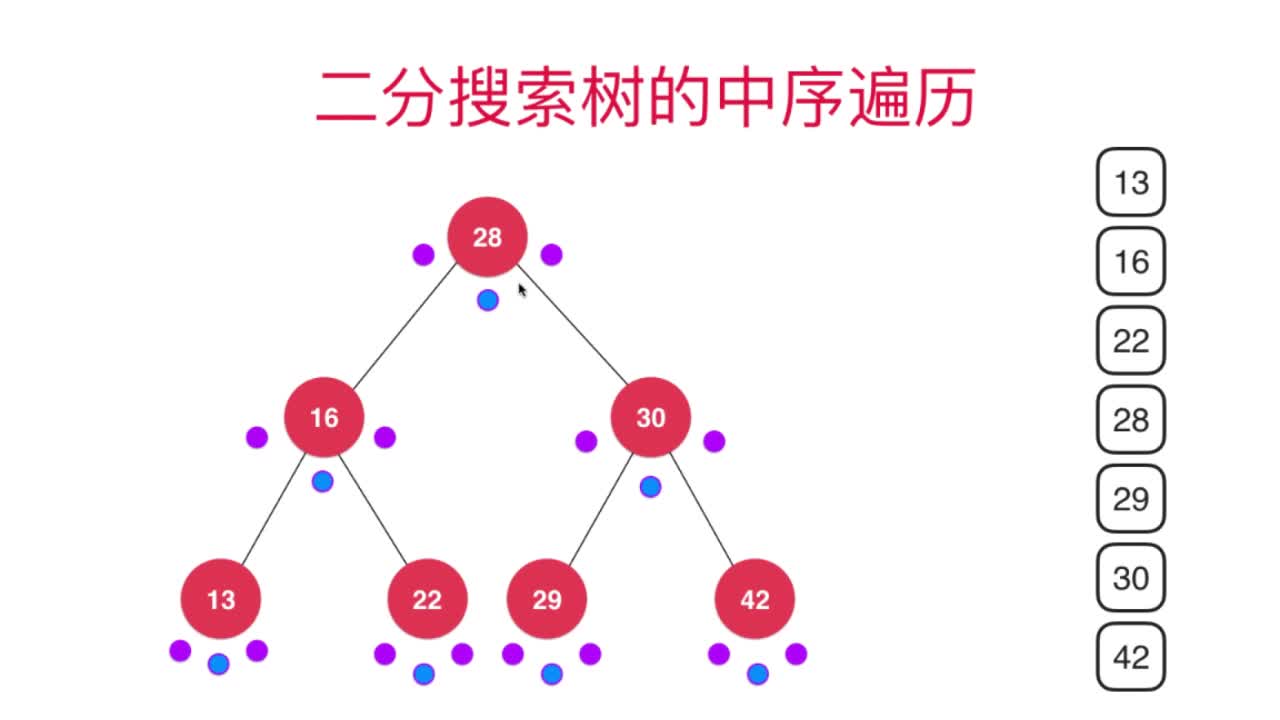

在遍历过程中每个节点都访问了3次，对应着这3个小点，顺序为前-> 中 -> 后，只有在“中”点时才会打印该节点元素值（即上图中蓝色的点）。
由于二叉搜索树的定义，中序遍历的输出其实是元素从小到大的输出，因此在进行实际应用时，可使用二叉搜索树的中序遍历将元素按照从小到大顺序输出。

后序遍历：先递归访问左右子树，再访问自身节点
可以参考下图进行理解：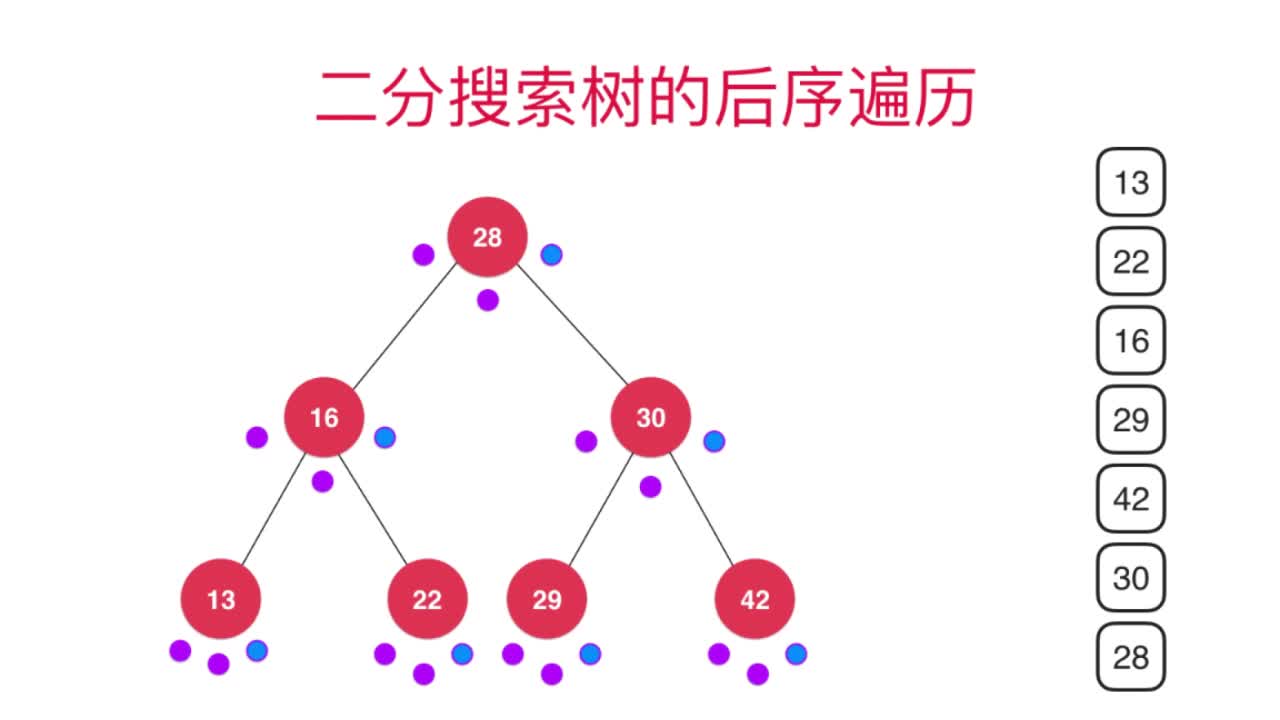

在遍历过程中每个节点都访问了3次，对应着这3个小点，顺序为前-> 中 -> 后，只有在“后”点时才会打印该节点元素值（即上图中蓝色的点）。

代码实现见清单1.

二叉搜索树的广度优先遍历（层序遍历）

上面提到的前序、中序、后序遍历都属于深度优先遍历，遍历一开始首先会走到最深，再回溯到开始遍历整棵树。
而广度优先遍历则是层序遍历，一层一层地向下遍历，其实很好理解，广度优先就是先把当前层都遍历完了才开始下一层，深度优先则是先沿一条路走到底，再回来走其他路 : )
二叉搜索树的广度优先遍历的实现，借助了一个队列，首先是先将根节点入队，然后取出队列中第一个节点（也就是根节点），然后分别判断是否有左右子节点，如果有则入队。
二叉树的广度优先遍历可以参考下图进行理解：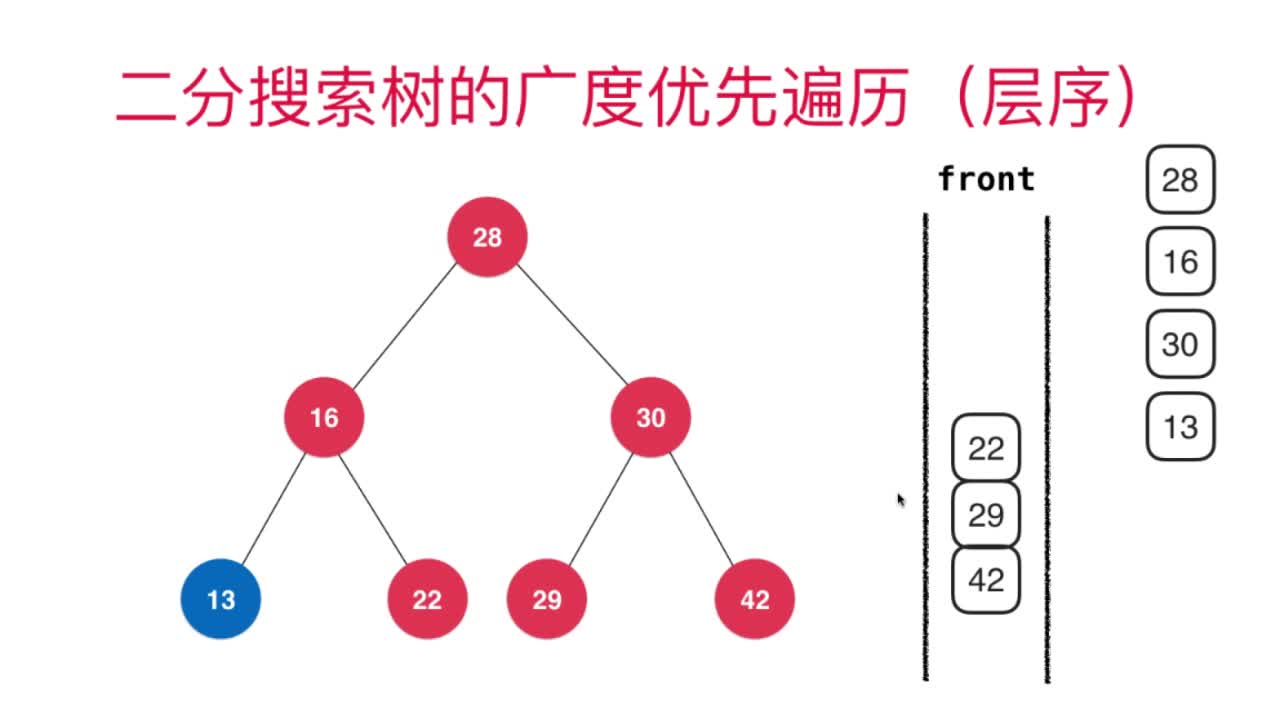

根节点出队，子节点就入队，根据队列先进先出的性质，就实现了一个广度优先的二分搜索树的遍历。
注意：当循环到最底下的时候，因为再没有子节点了，所以最下层的节点全部出队即可。

二叉搜索树的删除操作

删除操作是二叉搜索树中最难的操作，其实查找需要删除的节点和删除本身不难，难的是在待删除节点有左右子树的时候，如何操作才能使删除后整棵树仍然保持二叉搜索树的性质。
先来看看简单的情况，删除最小值和最大值。
删除最小值
删除最小值，根据二叉搜索树的定义或者特点，我们很容易可以得出，其实就是要删除最左边的节点；
也就是从根节点开始递归的往左子树寻找，直到某一个节点的左子树为空，那么该节点就是最小的节点了,那么该节点可能有右节点，也可能没有右节点；当该节点有右节点时，需要把右节点返回。
注意下面代码中的待删除节点的右节点可能是为空的，不过这并不影响，正好两种情况都包含在内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public:
    void removeMin()
    {
        if(root)
            root = removeMin(root);
    }
private:
    Node* removeMin(Node* node)
    {
        if(NULL == node->left)
        {
            Node* rightNode = node->right;
            delete node;
            count--;

            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

删除最大值则是往右子树递归到最右边即可，在此省略

其实通过描述，也可以发现，这两个地方可以不用递归的方式实现，有兴趣的读者可以试试用非递归的方式实现: )

删除指定节点

如果待删除节点只有1个孩子节点或者没有孩子节点，那么删除该节点操作与删除最大值最小值的操作无异，在删除该节点之后，其孩子节点可以顶替。
我们需要真正考虑的是，如果待删除节点有左右孩子节点（有左右子树）时要如何操作。
幸运的是，这个难题前人Hubbard已经帮我们解决了，其实当有左右孩子时需要找合适的节点来替代当前节点，使得整棵二叉搜索树性质不变。
Hubbard认为替代删除节点的合适节点是待删除节点的右子树中最小节点。因此，整个过程可以总结为首先寻找待删除节点的后继节点（右子树中的最小值），由后继节点代替待删除节点即可。该算法也被叫做Hubbard Deletion算法。

删除节点过程可以参考下图进行理解



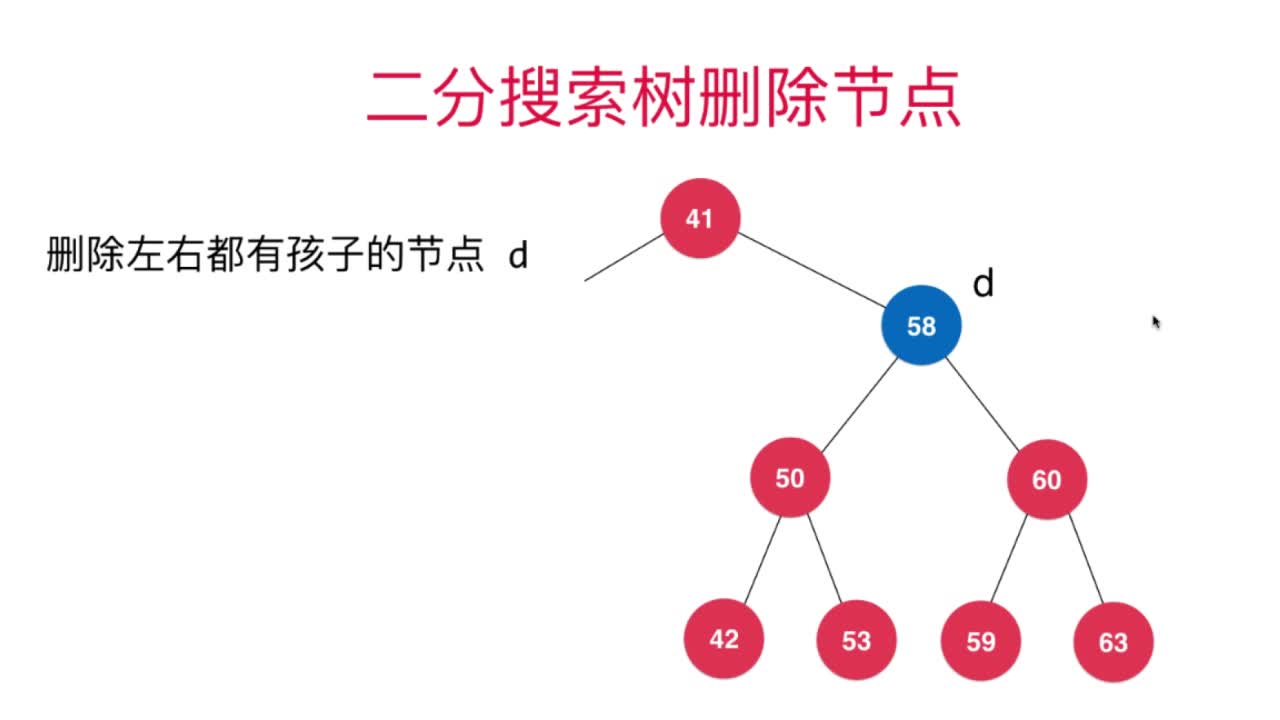
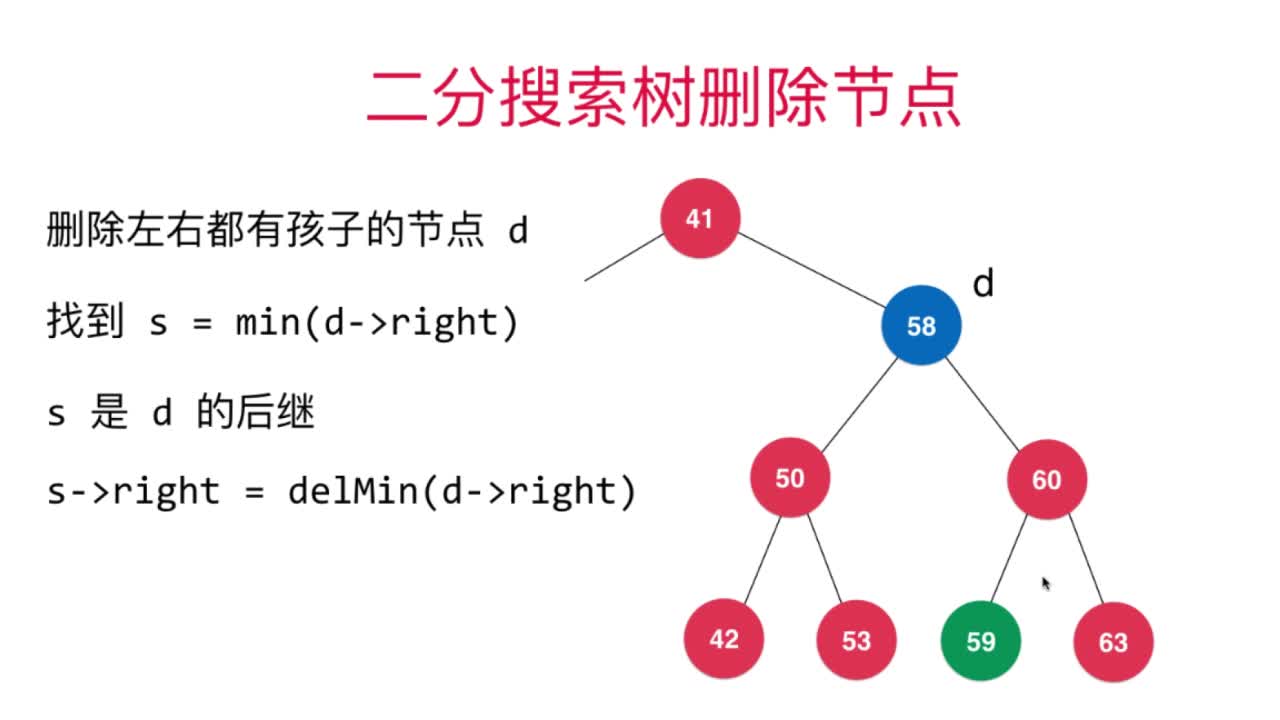
如图，59便是s节点，也是d节点的后继节点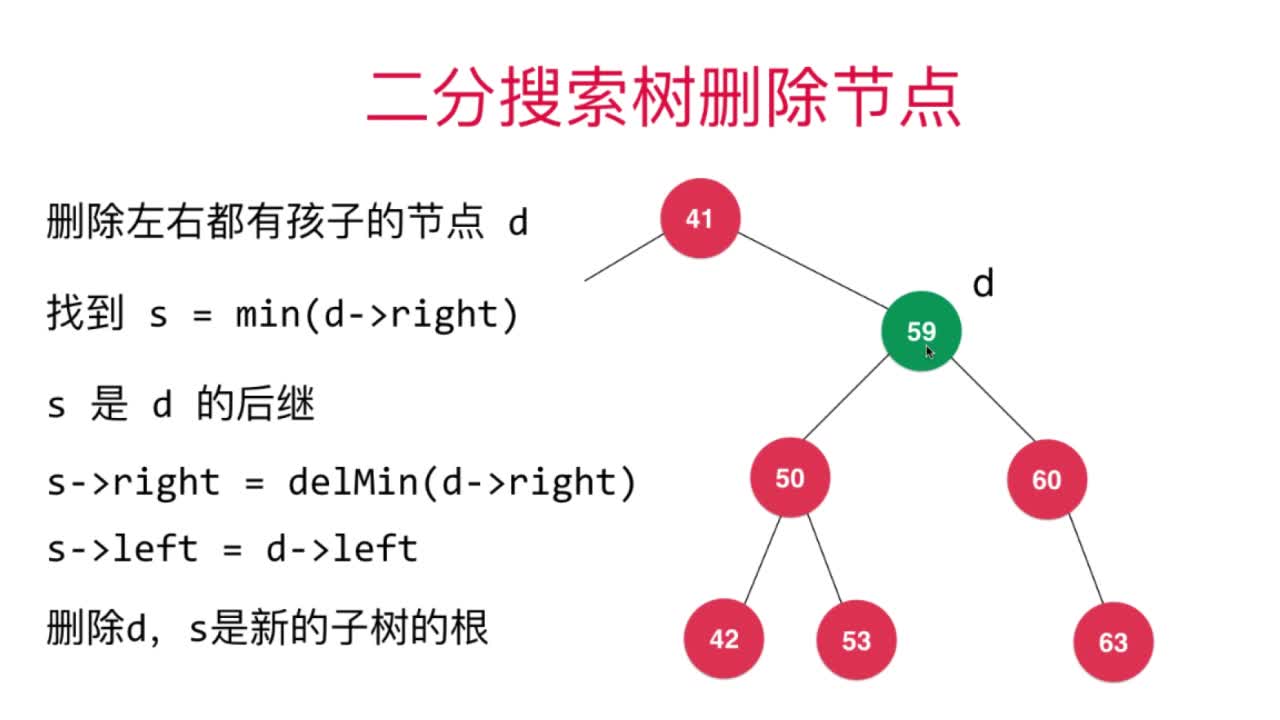

代码见清单1.

二叉搜索树的顺序性

除了上面提到的二叉搜索树的各种操作，大部分情况将二叉搜索树当作查找表来实现，主要关注的是如何查找一个key对应的value值，同时完成插入、删除、查找、遍历所有元素等操作。
注意二叉搜索树还有一个重要的特征：顺序性，也就是说不仅可以在二分搜索树中定位一个元素，还可以回答其顺序性相关的问题：
minimum , maximum：已经实现，非常容易可在一组数据中找到最小、大值。
successor , predecessor：待实现，可找到一个元素的前驱节点和后继节点。
floor , ceil：待实现
rank
select
感兴趣的读者可以尝试自行实现: )

二叉搜索树的局限性

二叉搜索树的局限性来源于在特殊情况下，二叉搜索树可能会退化成链表，其查找过程是与其高度相关，此时高度为n，时间复杂度为O(n)。
比如：下图所示，同样的数据，可以对应不同的二分搜索树。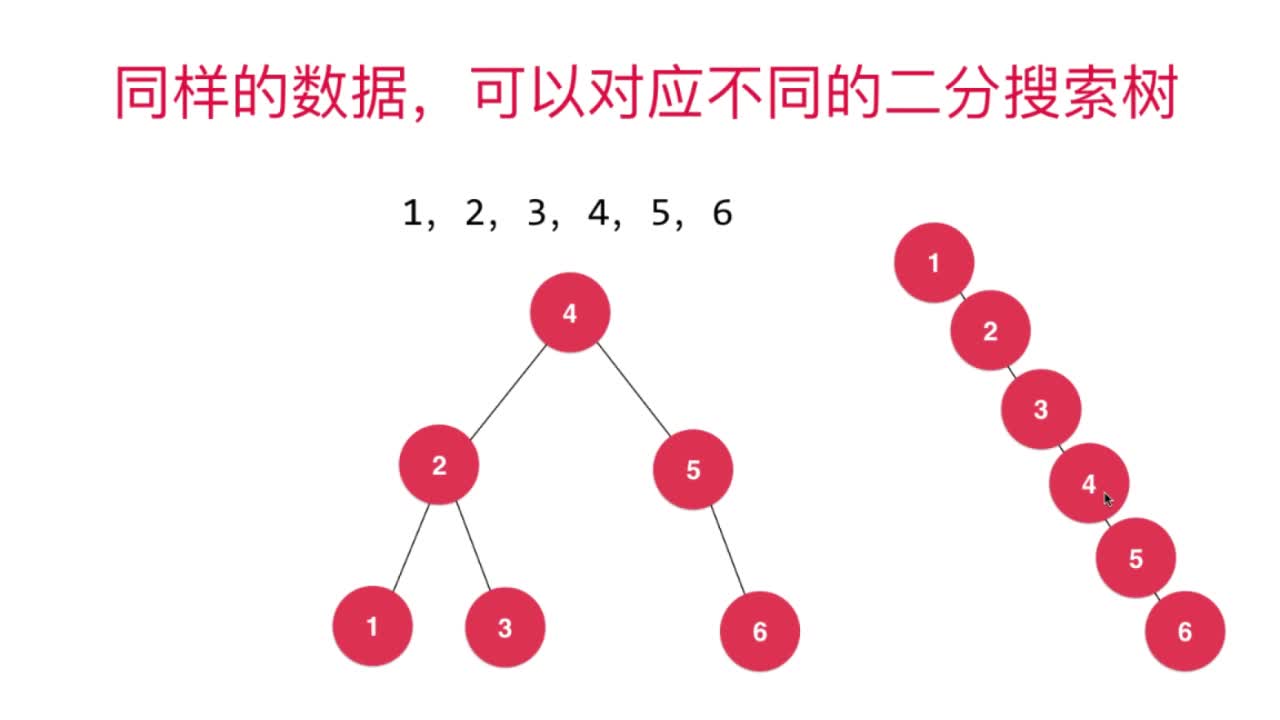

需要注意的是，二叉搜索树退化成链表后，但是在实现操作过程中还是有左孩子的概念，所以需要一直判断左孩子为空的情况，并且BST采用递归方式实现，其中的入栈出栈操作也会耗费一些时间，所以此时的二叉搜索树通常性能会比直接用链表性能要慢。

总结

总体来说二叉搜索树性能还是不错的，也很常用，需要掌握其各种操作。
关于二叉搜索树退化成链表的情况还是有解决办法的，可以改造二叉树的实现，使得其无法退化成链表，通常采用平衡二叉树，它有左右两棵子树，并且其高度差不会超过1，因此可以保证其高度一定是 logn 级别的，此概念的经典实现就是红黑树。

清单1 二叉搜索树的具体实现(包含上文的各种操作及测试程序)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
#include <iostream>
#include <queue>
#include <cassert>
#include <ctime>
#include <algorithm>

using namespace std;

template<typename Key, typename Value>
class BST
{
private:
    struct Node
    {
        Key key;
        Value value;
        Node* left;
        Node* right;

        Node(Key key, Value value)
        {
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }

        Node(Node *node)
        {
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
        }
    };

    Node* root;
    int count;

public:
    BST()
    {
        root = NULL;
        count = 0;
    }

    ~BST()
    {
        destroy(root);
    }

    int size()
    {
        return count;
    }

    bool isEmpty()
    {
        return count == 0;
    }

    void insert(Key key, Value value)
    {
        root = insert(root, key, value);
    }

    bool contain(Key key)
    {
        return contain(root, key);
    }

    Value* search(Key key)
    {
        return search(root, key);
    }

    void preOrder()
    {
        preOrder(root);
    }

    void inOrder()
    {
        inOrder(root);
    }

    void postOrder()
    {
        postOrder(root);
    }

    void levelOrder()
    {
        queue<Node*> q;
        q.push(root);
        while(!q.empty())
        {
            Node* node = q.front();
            q.pop();

            cout<<node->key<<endl;

            if(node->left)
            {
                q.push(node->left);
            }

            if(node->right)
            {
                q.push(node->right);
            }
        }
    }

    Key minimum()
    {
        assert(count != 0);
        Node* minNode = minimum(root);
        return minNode->key;
    }

    Key maxmum()
    {
        assert(count != 0);
        Node * maxNode = maxmum(root);
        return maxNode->key;
    }

    void removeMin()
    {
        if(root)
            root = removeMin(root);
    }

    void removeMax()
    {
        if(root)
           root = removeMax(root);
    }


    void remove(Key key)
    {
        if(root)
        {
            root = remove(root, key);
        }
    }


private:
    Node* insert(Node* node, Key key, Value value)
    {
        if(NULL == node)
        {
            count++;
            return new Node(key, value);
        }

        if(key == node->key)
        {
            node->value = value;
        }
        else if(key < node->key)
        {
            node->left = insert(node->left, key, value);
        }
        else
        {
            node->right = insert(node->right, key, value);
        }

        return node;
    }

    bool contain(Node* node, Key key)
    {
        if(NULL == node)
        {
            return false;
        }

        if(key == node->key)
        {
            return true;
        }
        else if(key < node->key)
        {
            return contain(node->left, key);
        }
        else
        {
            return contain(node->right, key);
        }
    }

    Value* search(Node* node, Key key)
    {
        if(NULL == node)
        {
            return NULL;
        }

        if(key == node->key)
        {
            return &(node->value);
        }
        else if(key < node->key)
        {
            return search(node->left, key);
        }
        else
        {
            return search(node->right, key);
        }
    }

    void preOrder(Node* node)
    {
        if(NULL != node)
        {
            cout<<node->key<<endl;
            preOrder(node->left);
            preOrder(node->right);
        }
    }

    void inOrder(Node* node)
    {
        if(NULL != node)
        {
            inOrder(node->left);
            cout<<node->key<<endl;
            inOrder(node->right);
        }
    }

    void postOrder(Node* node)
    {
        if(NULL != node)
        {
            postOrder(node->left);
            postOrder(node->right);
            cout<<node->key<<endl;
        }
    }

    void destroy(Node* node)
    {
        if(NULL != node)
        {
            destroy(node->left);
            destroy(node->right);

            delete node;
            count--;
        }
    }

    Node* minimum(Node* node)
    {
        if(NULL == node)
        {
            return NULL;
        }
        if(NULL == node->left)
        {
            return node;
        }
        else
        {
            return minimum(node->left);
        }
    }

    Node* removeMin(Node* node)
    {
        if(NULL == node->left)
        {
            Node* rightNode = node->right;
            delete node;
            count--;

            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    Node* removeMax(Node* node)
    {
        if(NULL == node->right)
        {
            Node* leftNode = node->left;
            delete node;
            count--;

            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }


    Node* remove(Node* node, Key key)
    {
        if(NULL == node)
        {
            return NULL;
        }

        if(key < node->key)
        {
            node->left = remove(node->left, key);
            return node;
        }
        else if(key > node->key)
        {
            node->right = remove(node->right, key);
            return node;
        }
        else //key == node->key
        {
            if(NULL == node->left)
            {
                Node* rightNode = node->right;
                delete node;
                count--;

                return rightNode;
            }

            if(NULL == node->right)
            {
                Node* leftNode = node->left;
                delete node;
                count--;
                return leftNode;
            }

            //node->left != NULL && node->right != NULL
            Node* successor = new Node(minimum(node->right));
            count++;

            successor->right = removeMin(node->right);
            successor->left = node->left;

            delete node;
            count--;

            return successor;
        }
    }


};


void shuffle(int arr[], int n)
{
    srand(time(NULL));
    for(int i = n-1; i >= 0; i--)
    {
        int x = rand()%(i+1);
        swap(arr[i], arr[x]);
    }
}


int main()
{
    srand(time(NULL));
    BST<int, int> bst = BST<int, int>();

    int n = 10000;
    for(int i = 0; i < n; i++)
    {
        int key = rand()%n;
        int value = key;
        bst.insert(key, value);
    }

    int order[n];
    for(int i = 0; i < n; i++)
    {
        order[i] = i;
    }

    shuffle(order, n);

    for(int i = 0; i < n; i++)
    {
        if(bst.contain(order[i]))
        {
            bst.remove(order[i]);
            cout<<"After remove "<<order[i]<<" size = "<<bst.size()<<endl;
        }
    }

    cout<<bst.size()<<endl;

    return 0;
}

参考资料

[算法（第4版）]
挖掘算法中的数据结构（七）：二分搜索树（删除、广度优先遍历、顺序性）及 衍生算法问题
可以看这篇文章的动图演示

如果你觉得本文对你有帮助，欢迎打赏