Redis源码阅读--跳跃表

发表于 | 分类于 | | 浏览 次
字数统计: 4,479 字 | 阅读时长 ≈ 22 分钟

本文主要介绍如下内容：

  • 跳跃表介绍
  • Redis中的跳跃表实现及特点
  • Redis中的跳跃表源码难点分析
  • Redis中的跳跃表源码部分节选

跳跃表介绍

跳跃表是一种随机化数据结构，基于并联的链表，其效率可以比拟平衡二叉树，查找、删除、插入等操作都可以在对数期望时间内完成，对比平衡树，跳跃表的实现要简单直观很多。

以下是一个跳跃表的例图(来自维基百科)：

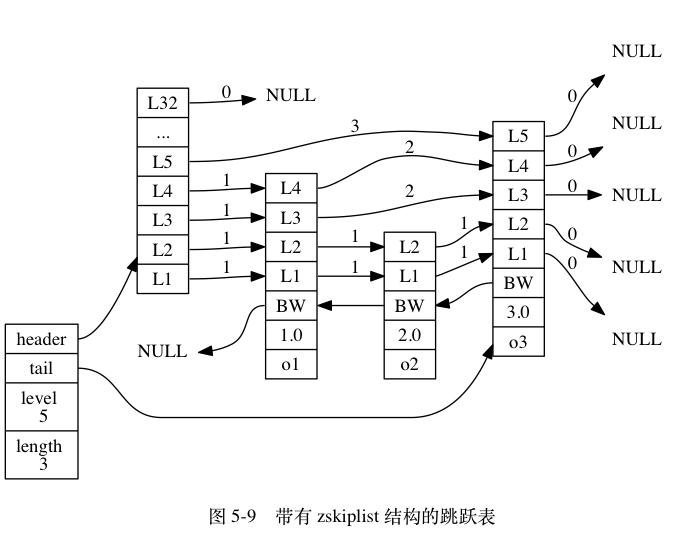
从图中可以看出跳跃表主要有以下几个部分构成：

1、 表头head：负责维护跳跃表的节点指针

2、 节点node：实际保存元素值，每个节点有一层或多层

3、 层level：保存着指向该层下一个节点的指针

4、 表尾tail：全部由null组成

跳跃表的遍历总是从高层开始，然后随着元素值范围的缩小，慢慢降低到低层。

Redis中的跳跃表实现及特点

Redis 的跳跃表由 redis.h/zskiplistNode 和 redis.h/zskiplist 两个结构体定义，具体实现在t_zset.c中。

跳跃表节点

1
2
3
4
5
6
7
8
9
10
/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    robj *obj;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

zskiplist 结构体

1
2
3
4
5
typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

header 和 tail 指针分别指向跳跃表的表头和表尾节点， 通过这两个指针， 程序定位表头节点和表尾节点的复杂度为 O(1) 。
通过使用 length 属性来记录节点的数量， 程序可以在 O(1) 复杂度内返回跳跃表的长度。
level 属性则用于在 O(1) 复杂度内获取跳跃表中层高最大的那个节点的层数量， 注意表头节点的层高并不计算在内。

特点

  • 跳跃表是有序集合的底层实现之一
  • Redis的跳跃表实现由 zskiplist 和 zskiplistNode两个结构组成,其中 zskiplist 用于保存跳跃表信息（比如表头节点、表尾节点、长度）， 而zskiplistNode则用于表示跳跃表节点
  • 每个跳跃表节点的层高都是 1 至 32 之间的随机数。
  • 在同一个跳跃表中， 多个节点可以包含相同的分值， 但每个节点的成员对象必须是唯一的。
  • 跳跃表中的节点按照分值大小进行排序， 当分值相同时， 节点按照成员对象的大小进行排序。

–
与通常描述的跳跃表的区别

Redis的跳跃表实现跟WilliamPugh在”Skip Lists: A Probabilistic Alternative to Balanced Trees”中描述的跳跃表算法类似，只是有如下不同：

  • 允许重复分数
  • 排序不止根据分数，还可能根据成员对象（当分数相同时）
  • 每个跳表节点中有backward指向前驱节点，从而可以方便的从表尾向表头遍历，用于ZREVRANGE命令的实现。

Redis中的跳跃表源码难点分析

随机算法函数

zslRandomLevel函数为我们要建的新跳表返回一个随机的层数，该数在1~32之间，且越大的数出现的概率越小。

1
2
3
4
5
6
7
8
9
10
/* Returns a random level for the new skiplist node we are going to create.
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. */
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

这里的ZSKIPLIST_P是0.25。上述代码中，level初始化为1，然后，如果持续满足条件：(random()&0xFFFF)< (ZSKIPLIST_P 0xFFFF)的话，则level+=1。最终调整level的值，使其小于ZSKIPLIST_MAXLEVEL。 理解该算法的核心，就是要理解满足条件：(random()&0xFFFF) < (ZSKIPLIST_P 0xFFFF)的概率是多少？
random()&0xFFFF形成的数，均匀分布在区间[0,0xFFFF]上，那么这个数小于(ZSKIPLIST_P 0xFFFF)的概率是多少呢？自然就是ZSKIPLIST_P，也就是0.25了。
因此，最终返回level为1的概率是1-0.25=0.75，返回level为2的概率为0.250.75，返回level为3的概率为0.250.250.75……因此，如果返回level为k的概率为x，则返回level为k+1的概率为0.25x，换句话说，如果k层的结点数是x，那么k+1层就是0.25x了。这就是所谓的幂次定律（powerlaw），越大的数出现的概率越小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef struct zskiplistNode {
    robj *obj;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

zskiplist *zslCreate(void);//创建一个新的跳跃表
void zslFree(zskiplist *zsl);//释放给定的跳跃表（包括表中所有节点）
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj);//将包含给定成员和分值的新节点插入到指定的跳跃表中


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}


void zslFree(zskiplist *zsl) {
    zskiplistNode *node = zsl->header->level[0].forward, *next;

    zfree(zsl->header);
    while(node) {
        next = node->level[0].forward;
        zslFreeNode(node);
        node = next;
    }
    zfree(zsl);
}

插入节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    redisAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. */
    level = zslRandomLevel();
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,obj);
    for (i = 0; i < level; i++) {
        /*update[i]中记录了在i层插入节点应该插入的位置，所以x的后继节点就应该是当前  
        update[i]->level[i]的后继节点了*/
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;//将x插入到update[i]->level[i]后

        /* update span covered by update[i] as x is inserted here */
        /*跨度span用于记录当前节点的forward指针指向的节点和当前节点的距离，
        所以应该等于该节点在第i层上的后继节点(forward指针指向的节点)的排名，  
        减去该节点的排名,新结点在第i层的后继节点，也就是之前update[i]的后继节点，
        它的排名是update[i]->level[i].span+ rank[i]，插入新结点之后，
        它的排名加1，也就是update[i]->level[i].span + rank[i] + 1。
        新结点的排名，就是rank[0]+ 1，因此，新结点在第i层的层跨度就是
        (update[i]->level[i].span + rank[i] + 1) – (rank[0] + 1)，
        也就是update[i]->level[i].span- (rank[0] - rank[i])。*/
        
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        
        /*前驱结点update[i]的层跨度，等于新结点的排名rank[0]+ 1，
        减去update[i]的排名rank[i]，也就是(rank[0] + 1) - rank[i]，
        也就是(rank[0] -rank[i]) + 1*/
        
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

关于插入节点这个函数的实现，我们需要明白几点，在知道zskiplistNode和zskiplist数据结构的基础上，把以下几点弄明白了，整个函数就好理解了。

  1. 辅助数组update的作用是什么
  2. 数组rank的作用是什么
  3. 哪些层需要插入该节点
  4. 结构体zskiplistNode中span的意义是什么

第1个问题：首先我们要插入一个节点，与链表类似，需要找到合适位置插入，而辅助数组update就用来存放待插入节点在每一层应该插入的位置的,即代码开头这一段：

1
2
3
4
5
6
7
8
9
10
11
12
13
x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }

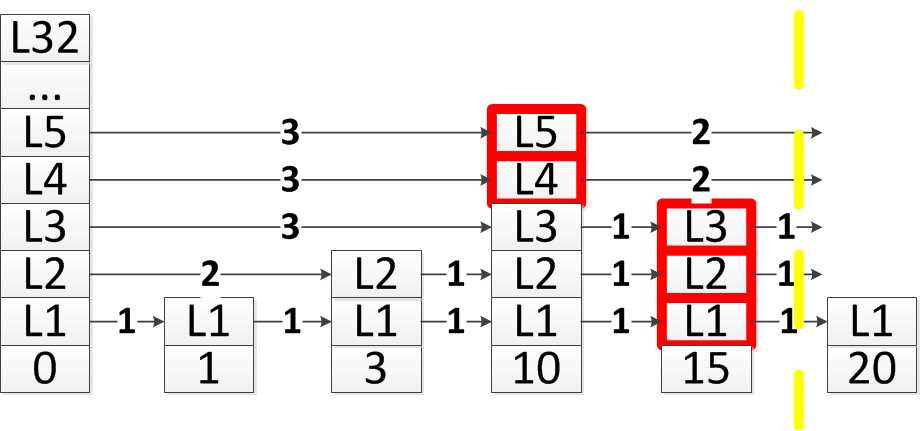
第2个问题，数组rank用来存放的是每层合适的待插入位置的排名，比如在下图的跳跃表中，假设现在要插入的结点分数为17，黄色虚线所标注的，就是插入新结点的位置。下面标注红色的，就是在每层找到的插入结点的前驱结点，记录在update[i]中，而rank[i]记录了update[i]在跳跃表中的排名，因此，rank[4] = 3, rank[3] = 3, rank[2] = 4, rank[1] = 4, rank[0] = 4

第3个问题哪些层需要插入这个节点，这个问题在Redis中是采用了前面说的随机算法，利用随机算法得出一个在1~32之间的level值，第0层到第level-1层都需要插入该节点：

1
2
3
4
5
6
7
8
9
level = zslRandomLevel();
if (level > zsl->level) {
    for (i = zsl->level; i < level; i++) {
        rank[i] = 0;
        update[i] = zsl->header;
        update[i]->level[i].span = zsl->length;
    }
    zsl->level = level;
}

第4个问题：zskiplistNode中span表示跨度，用于记录当前节点的forward指针指向的节点和当前节点的距离（如果指向 NULL，那么前进指针的跨度都为0，因为它们没有连向任何节点）。此外，由于排名rank是由前面各span累积起来的，比如上面给的图中的值为10的节点的排名就是3，所以我们在计算当前节点的span的时候，可以用后继节点排名减去当前节点节点排名，下面这段代码就用了这个逻辑：

1
2
3
4
5
6
7
8
9
x = zslCreateNode(level,score,obj);
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

最后这段代码就好理解了，只需要看结构图就明白了

1
2
3
4
5
6
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
    x->level[0].forward->backward = x;
else
    zsl->tail = x;
zsl->length++;

结构图：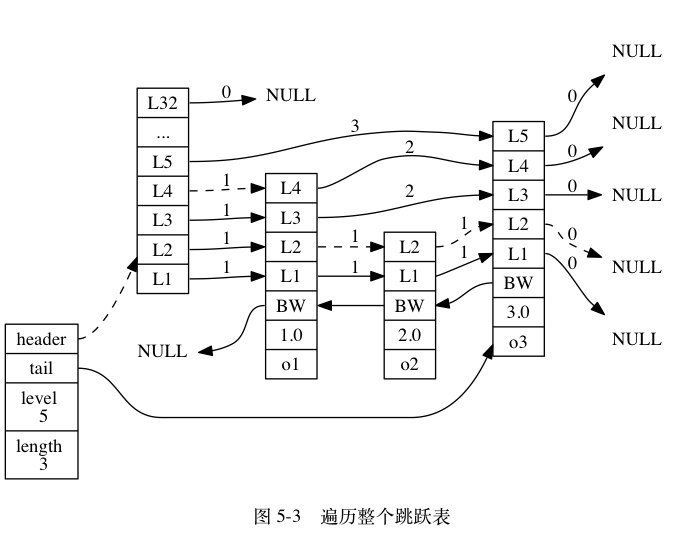

即如果update[0] == zsl->header，那么根据图，它的backward就应该为NULL；
如果x->level[0].forward为NULL，那表明该节点为尾节点，所以zsl->tail = x。

Redis中的跳跃表源码部分节选

删除跳表中匹配score和obj的节点
理解了上面的插入节点，这个部分是很好看懂的，请看源码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}

/* Delete an element with matching score/object from the skiplist. */
int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0)))
            x = x->level[i].forward;
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj,obj)) {
        zslDeleteNode(zsl, x, update);
        zslFreeNode(x);
        return 1;
    }
    return 0; /* not found */
}

获取某一score和成员对象o对应的节点的排名

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/* Find the rank for an element by both score and key.
 * Returns 0 when the element cannot be found, rank otherwise.
 * Note that the rank is 1-based due to the span of zsl->header to the
 * first element. */
unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,o) <= 0))) {
            rank += x->level[i].span;
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        if (x->obj && equalStringObjects(x->obj,o)) {
            return rank;
        }
    }
    return 0;
}

需要注意的是在同一个跳跃表中， 各个节点保存的成员对象必须是唯一的， 但是多个节点保存的分值却可以是相同的，否则上面的实现是有问题的，如果没有这一限制，如果在该跳表中只有一个大于score，且成员对象也为o的节点，那么此时会返回rank，而这个时候其实是应该返回0，即表示没有找到相应的节点。由于已经限定没有重复o，所以上述实现正确。

根据排名找对应的节点:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* Finds an element by its rank. The rank argument needs to be 1-based. */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x;
    unsigned long traversed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        if (traversed == rank) {
            return x;
        }
    }
    return NULL;
}


结构体zrangespec
该结构体给出一个score的范围min~max,minex和maxex是用来表示这个范围区间开闭的,为0表示包括，为1表示不包括。如果要表示[10, 15]，那么
1
2
3
zrangespec.min = 10;
zrangespec.max = 15;
zrangespec.minex = zrangespec.maxex = 0;

1
2
3
4
5
/* Struct to hold a inclusive/exclusive range spec by score comparison. */
typedef struct {
    double min, max;
    int minex, maxex; /* are min or max exclusive? */
} zrangespec;

给定一个分值范围， 返回跳跃表中第一个符合这个范围的节点:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/* Returns if there is a part of the zset is in range. */
int zslIsInRange(zskiplist *zsl, zrangespec *range) {
    zskiplistNode *x;

    /* Test for ranges that will always be empty. */
    if (range->min > range->max ||
            (range->min == range->max && (range->minex || range->maxex)))
        return 0;
    x = zsl->tail;
    if (x == NULL || !zslValueGteMin(x->score,range))
        return 0;
    x = zsl->header->level[0].forward;
    if (x == NULL || !zslValueLteMax(x->score,range))
        return 0;
    return 1;
}

/* Find the first node that is contained in the specified range.
 * Returns NULL when no element is contained in the range. */
zskiplistNode *zslFirstInRange(zskiplist *zsl, zrangespec *range) {
    zskiplistNode *x;
    int i;

    /* If everything is out of range, return early. */
    if (!zslIsInRange(zsl,range)) return NULL;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* Go forward while *OUT* of range. */
        while (x->level[i].forward &&
            !zslValueGteMin(x->level[i].forward->score,range))
                x = x->level[i].forward;
    }

    /* This is an inner range, so the next node cannot be NULL. */
    x = x->level[0].forward;
    redisAssert(x != NULL);

    /* Check if score <= max. */
    if (!zslValueLteMax(x->score,range)) return NULL;
    return x;
}

给定一个分值范围， 返回跳跃表中最后一个符合这个范围的节点:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/* Find the last node that is contained in the specified range.
 * Returns NULL when no element is contained in the range. */
zskiplistNode *zslLastInRange(zskiplist *zsl, zrangespec *range) {
    zskiplistNode *x;
    int i;

    /* If everything is out of range, return early. */
    if (!zslIsInRange(zsl,range)) return NULL;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* Go forward while *IN* range. */
        while (x->level[i].forward &&
            zslValueLteMax(x->level[i].forward->score,range))
                x = x->level[i].forward;
    }

    /* This is an inner range, so this node cannot be NULL. */
    redisAssert(x != NULL);

    /* Check if score >= min. */
    if (!zslValueGteMin(x->score,range)) return NULL;
    return x;
}


给定一个分值范围， 删除跳跃表中所有在这个范围之内的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/* Delete all the elements with score between min and max from the skiplist.
 * Min and max are inclusive, so a score >= min || score <= max is deleted.
 * Note that this function takes the reference to the hash table view of the
 * sorted set, in order to remove the elements from the hash table too. */
unsigned long zslDeleteRangeByScore(zskiplist *zsl, zrangespec *range, dict *dict) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long removed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (range->minex ?
            x->level[i].forward->score <= range->min :
            x->level[i].forward->score < range->min))
                x = x->level[i].forward;
        update[i] = x;
    }

    /* Current node is the last with score < or <= min. */
    x = x->level[0].forward;

    /* Delete nodes while in range. */
    while (x &&
           (range->maxex ? x->score < range->max : x->score <= range->max))
    {
        zskiplistNode *next = x->level[0].forward;
        zslDeleteNode(zsl,x,update);
        dictDelete(dict,x->obj);
        zslFreeNode(x);
        removed++;
        x = next;
    }
    return removed;
}


需要注意的是minex为1表示包括左边是开区间，为0表示闭区间，maxex为1表示右边为开区间，为0表示闭区间。

删除排名在[start, end]之间的所有节点，包含start和end

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/* Delete all the elements with rank between start and end from the skiplist.
 * Start and end are inclusive. Note that start and end need to be 1-based */
unsigned long zslDeleteRangeByRank(zskiplist *zsl, unsigned int start, unsigned int end, dict *dict) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long traversed = 0, removed = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward && (traversed + x->level[i].span) < start) {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }

    traversed++;
    x = x->level[0].forward;
    while (x && traversed <= end) {
        zskiplistNode *next = x->level[0].forward;
        zslDeleteNode(zsl,x,update);
        dictDelete(dict,x->obj);
        zslFreeNode(x);
        removed++;
        traversed++;
        x = next;
    }
    return removed;

参考资料

Redis设计与实现
Redis源码3.0.6
漫画算法：什么是跳跃表？
浅析SkipList跳跃表原理及代码实现
Redis源码解析：05跳跃表
__typeof__() 、 __typeof（） 、 typeof（）的区别

如果你觉得本文对你有帮助，欢迎打赏